Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 2:
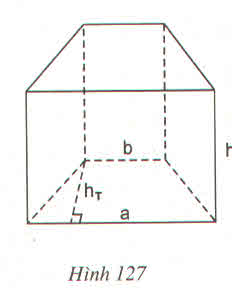
Gọi a;b là 2 kích thước còn lại của hình hộp chữ nhật. Theo đề bài ta có:
2(a+b).h = 120
<=> 2.(a+b).6=120
<=> a+b= 10 (cm)
V lớn nhất <=> a.b.h lớn nhất<=> a.b lớn nhất mà ab < hoặc = (a+b)^2/4
Nên V lớn nhất khi a=b= 10/2=5 (cm)
Vậy V đạt giá trị lớn nhất là 5.5.6= 150 cm3 khi các kích thước của đáy bằng 5 cm
Câu 2: giải
Gọi a, b là kích thước của đáy
Tcó V=6ab nên V lớn nhất \(\Leftrightarrow\)ab lớn nhất
\(S_{xq}=120\)nên 2(a+b).6=120 hay a+b=10
Tcó ab=a(10-a)= \(-a^2+10a=-\left(a-5\right)^2+25\le25\)
Sra V=6ab\(\le\)6.25=150
Vậy thể tích lớn nhất =150\(cm^3\) khi a=b=5, tức là các cạnh đáy =5cm
CHÚC BẠN HỌC TỐT, good luck:)

diện tích xung quanh của lăng trụ là (\(\sqrt{53}\times2+11+15)\)\(\times\)14\(\approx\)567,8mm2

A B C 3 4 H I D
a, C/m ΔABC ∼ ΔHAC ⇒ AC2 = CH . BC
Xét ΔvABC và ΔvHAC. Ta có: \(\widehat{ACB}\) chung (gt)
⇒ ΔABC ∼ ΔHAC
Nên: \(\frac{AC}{CH}=\frac{BC}{AC}\)
⇒ AC2 = CH . BC
b, Tính AD, DB?
Ta có: ΔABC vuông tại A (gt)
⇒ BC2 = AB2 + AC2 = 32 + 42 = 25
Nên: BC = \(\sqrt{25}=5\left(cm\right)\)
Mà: CD là tia phân giác của \(\widehat{ACB}\) (gt)
⇒ \(\frac{AD}{AC}=\frac{DB}{BC}\)
Nên: \(\frac{AD}{AC}=\frac{DB}{BC}=\frac{AD+DB}{AC+BC}=\frac{AB}{AC+BC}\)
Hay: \(\frac{AD}{4}=\frac{DB}{5}=\frac{3}{4+5}=\frac{1}{3}\)
⇒ \(AD=\frac{4}{3}\left(cm\right)\)
\(DB=\frac{5}{3}\left(cm\right)\)
Cho hình chữ nhật ABCD. Vẽ AH vuông góc BD (H\(\in\)BD), HK//CD (K\(\in\)BC).
a) CM: tam giác ADH đồng dạng với tam giác DBC
b) CM: CD.BK=AH.BH
c) Cho biết AB=5cm, HB=4cm. Tính BK?
Tam giác vuông ABB' có B A B ' ^ = 45 0 nên là tam giác vuông cân tại B nên AB = BB' = 2cm.
Vì ABC là tam giác đều nên chu vi đáy bằng 6( cm )
Khi đó diện tích xung quanh hình lăng trụ là S x q = 6 . 2 = 12 ( c m 2 )
Chọn đáp án C.