Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Dùng phương pháp tọa độ hóa.
Đặt hệ trục tọa độ, ở đây như thầy đã trình bày ta nên chọn gốc tại P trục Ox, Oy là PA và PC.
Gọi α góc tạo bởi hai mặt phẳng ( AB'C' ) và (MNP)
Khi đó cos α = n 1 → . n 2 → n 1 → . n 2 → = 13 65
Đáp án cần chọn là B
Bài 3:
Do a và b đều không chia hết cho 3 nhưng khi chia cho 3 thì có cùng số dư nên\(\left[{}\begin{matrix}\left\{{}\begin{matrix}a=3n+1\\b=3m+1\end{matrix}\right.\\\left\{{}\begin{matrix}a=3n+2\\b=3m+2\end{matrix}\right.\end{matrix}\right.\)
TH1:\(\left\{{}\begin{matrix}a=3n+1\\b=3m+1\end{matrix}\right.\)
\(\Rightarrow ab-1=\left(3n+1\right)\left(3m+1\right)-1\)
\(\Rightarrow ab-1=9nm+3m+3n+1-1=9nm+3m+3n⋮3\) nên là bội của 3 (đpcm)
TH2:\(\left\{{}\begin{matrix}a=3n+2\\b=3m+2\end{matrix}\right.\)
\(\Rightarrow ab-1=\left(3n+2\right)\left(3m+2\right)-1\)
\(\Rightarrow ab-1=9nm+6m+6n+4-1=9nm+6m+6n+3⋮3\) nên là bội của 3 (đpcm)
Vậy ....
Bài 2:
\(B=\frac{1}{2010.2009}-\frac{1}{2009.2008}-\frac{1}{2008.2007}-...-\frac{1}{3.2}-\frac{1}{2.1}\)
\(\Rightarrow B=\frac{1}{2010.2009}-\left(\frac{1}{2009.2008}+\frac{1}{2008.2007}+...+\frac{1}{3.2}+\frac{1}{2.1}\right)\)
Đặt A=\(\frac{1}{2009.2008}+\frac{1}{2008.2007}+...+\frac{1}{3.2}+\frac{1}{2.1}\)
\(\Rightarrow A=\frac{2009-2008}{2009.2008}+\frac{2008-2007}{2008.2007}+...+\frac{3-2}{3.2}+\frac{2-1}{2.1}\)
\(\Rightarrow A=\frac{2-1}{2.1}+\frac{3-2}{3.2}+...+\frac{2008-2007}{2008.2007}+\frac{2009-2008}{2009.2008}\)
\(\Rightarrow A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{2007}-\frac{1}{2008}+\frac{1}{2008}-\frac{1}{2009}\)
\(\Rightarrow A=1-\frac{1}{2009}\)
\(\Rightarrow B=\frac{1}{2010.2009}-A=\frac{1}{2010.2009}-\left(1-\frac{1}{2009}\right)\)
\(\Rightarrow B=\frac{1}{2010.2009}+\frac{1}{2009}-1=\frac{2011}{2010.2009}-1\)
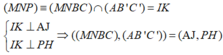
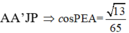
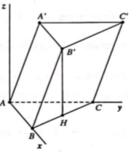
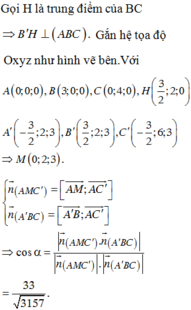
Đáp án A.
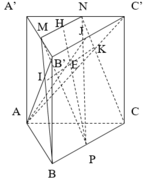
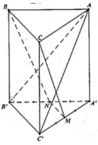
Cách 1: Gọi P là giao điểm của BN và A'B'=>P là trọng tâm Δ A ' B ' B .
Q là giao điểm của CM và A'C'=>Q là trọng tâm Δ A ' C ' C
⇒ P Q / / B ' C ' Ta có A B ' C ' ∩ B C M N = P Q .
Gọi H là trung điểm của B'C' và I là giao điểm của AH và PQ.
I là trung điểm của PQ.
Qua I kẻ đường thẳng vuông góc với BC, cắt BC và MN lần lượt tại J và K
=>J là trung điểm BC và K là trung điểm MN.
Ta có A B ' = A C ' ⇒ Δ A B ' C ' cân tại A ⇒ A H ⊥ B C ⇒ A I ⊥ P Q .
Lại có I J ⊥ P Q ⇒ Góc giữa A B ' C ' và B C M N là góc giữa IJ và IA.
Ta có:
A C ' = A C 2 + C C ' 2 = 2 3 2 + 2 2 = 4
⇒ A H = A C ' 2 − H C ' 2 = 4 2 − 3 2 = 13 ⇒ A I = 2 3 A H = 2 13 3
B N = B B ' 2 + B ' N 2 = 2 2 + 3 2 = 7
K J = N E = B N 2 − E B 2 = 7 − 3 4 = 5 2 ⇒ I J = 2 3 K J = 5 3
Lại có A J = 2 3 . 3 2 = 3
Trong Δ A I J :
cos A I J ^ = I J 2 + I A 2 − A J 2 2. I J . I A = 25 9 + 4.13 9 − 9 2. 5 3 . 2 13 3 = − 13 65 .
Cosin của góc giữa A B ' C ' và B C M N là 13 65
Cách 2: (Tọa độ hóa)
Gọi T là trung điểm AC. Đặt M = 0 ; 0 ; 0 , B ' 3 ; 0 ; 0 , C ' 0 ; 3 ; 0 , T 0 ; 0 ; 2
⇒ A 0 ; − 3 ; 2 , B 3 ; 0 ; 2 , C 0 ; 3 ; 2 ⇒ M B → = 3 ; 0 ; 2 , M C → = 0 ; 3 ; 2
n → = M B → , M C → = 2 3 ; 6 ; 6 3 là một vecto pháp tuyến của .
Lại có A B ' → = 3 ; 3 ; − 2 , A C ' → = 0 ; 2 3 ; − 2
⇒ n ' → = A B → , A C → ' = 2 3 ; 6 ; 6 3 là một vecto pháp tuyến của A B ' C ' .
Gọi α là góc giữa A B ' C ' và M N B C .
Ta có:
cos α = cos n → ; n ' → ^ = − 2 3 .2 3 + − 6 .6 + 3 3 .6 3 − 2 3 2 + − 6 2 + 3 3 2 . 2 3 2 + 6 2 + 6 3 2 = 13 65