Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

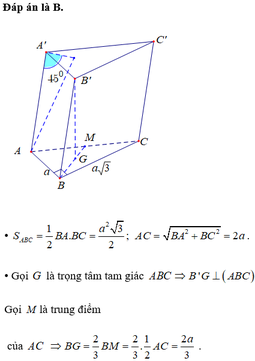
Gọi M là trung điểm BC: BC = 2a; AG = 2 3 AI = 2 a 3 ; A ' A G ^ = 60 o .
Suy ra: A ' G = A G tan 60 o = 2 a 3 3
Ta có: V = S A B C . A ' G = 1 2 AB.AC.A'G
= 1 2 a. a 3 . 2 a 3 3 = a 3
Vậy V 3 + V a 3 - 1 = a
Đáp án B

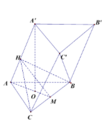
Gọi M là trung điểm BC. Từ M kẻ M H ⊥ A A ' ⇒ H B C ⊥ A A '
H M = 2 d t H B C B C = 2 a 2 3 8 a = a 3 4
A H = A M 2 - H M 2 = 3 a 2 4 - 3 a 2 16 = 3 a 4
∆ A M H ~ ∆ A A ' O ⇒ A H A O = M H A ' O ⇒ A ' O = A O . M H A H = a . a 3 . 4 3 . 4 . 3 a = a 3
Vậy thể tích ABCA’B’C' là
V = A O . d t A B C = a 3 . a 2 3 4 = a 3 3 12
Đáp án cần chọn là D






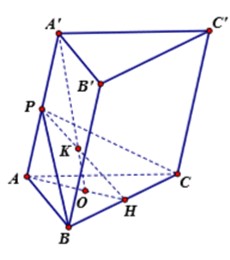
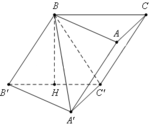

Đáp án D
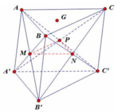
Gọi M là giao điểm của AI và BC; gọi N là giao điểm của A'J và B'C'. Suy ra M,N lần lượt là trung điểm của BC,B'C'.
Ta có M N / / B B ' A A ' / / B B ' ⇒ M N / / A A ' . Mặt khác M N = B B ' ⇒ M N = A A ' .
Từ hai dữ kiện trên suy ra AMNA' là hình bình hành. Vậy thiết diện tạo bởi mặt phẳng (ẠIJ) và hình lăng trụ là hình bình hành.