Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Xét lăng trụ (T) có:
![]()
Xét mặt cầu (C) có: R C = A P 2 = a 3
![]()
Tỉ số bằng 8 4 3 = 2 3 3

Đáp án A
A B C D . A ' B ' C ' D ' nội tiếp khối lăng trụ, ABCD.MNPQ nội tiếp mặt cầu nên
A B C D . A ' B ' C ' D ' là hình hộp chữ nhật
Bán kính đường tròn ngoại tiếp
ABCD là r = 2 a , V T = 4 a . π . 2 a 2 = 8 πa 3
Bán kính mặt cầu ngoại tiếp ABCD.MNPQ là
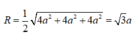
![]()
Vậy V ( T ) V ( C ) = 8 πa 3 4 3 πa 3 = 2 3 3

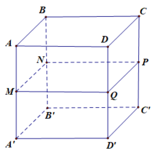
A B C B' C' A' E M
Từ giả thiết ta suy ra tam giác ABC là tam giác vuông cân tại B
Thể tích của khối lăng trụ là \(V_{ABC.A'B'C'}=AA'.BC=a\sqrt{2.}\frac{1}{2}a^2=\frac{\sqrt{2}}{2}a^3\)
Gọi E là trung điểm của BB'. Khi đó mặt phẳng (AME) song song với B'C nên khoảng cách giữa 2 đường thẳng AM, B'C bằng khoảng cách giữa B'C và mặt phẳng (AME)
Nhận thấy, khoảng cách từ B đến mặt phẳng (AME) bằng khoảng cách từ C đến mặt phẳng (AME)
Gọi h là khoảng cách từ B đến mặt phẳng (AME). Do đó tứ diện BAME có BA, BM, BE đôi một vuông góc với nhau nên :
\(\frac{1}{h^2}=\frac{1}{BA^2}+\frac{1}{BM^2}+\frac{1}{BE^2}\Rightarrow\frac{1}{h^2}=\frac{1}{a^2}+\frac{4}{a^2}+\frac{2}{a^2}=\frac{7}{a^2}\)
\(\Rightarrow h=\frac{a\sqrt{7}}{7}\)
Vậy khoảng cách giữa 2 đường thẳng B'C và AM bằng \(\frac{a\sqrt{7}}{7}\)
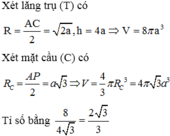
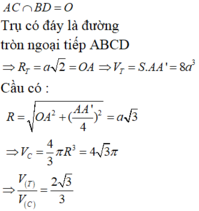
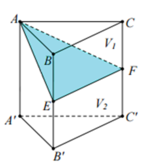
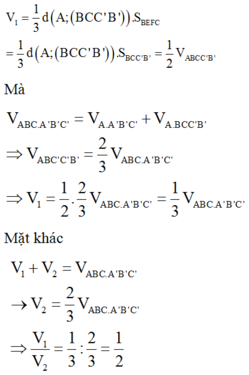
Chọn A.
Để ý rằng hai khối lăng trụ đó có diện tích đáy bằng nhau, tỉ số hai đường cao tương ứng bằng 1/2.
a.1/2
okkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkk