Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C 3 4 H I D
a, C/m ΔABC ∼ ΔHAC ⇒ AC2 = CH . BC
Xét ΔvABC và ΔvHAC. Ta có: \(\widehat{ACB}\) chung (gt)
⇒ ΔABC ∼ ΔHAC
Nên: \(\frac{AC}{CH}=\frac{BC}{AC}\)
⇒ AC2 = CH . BC
b, Tính AD, DB?
Ta có: ΔABC vuông tại A (gt)
⇒ BC2 = AB2 + AC2 = 32 + 42 = 25
Nên: BC = \(\sqrt{25}=5\left(cm\right)\)
Mà: CD là tia phân giác của \(\widehat{ACB}\) (gt)
⇒ \(\frac{AD}{AC}=\frac{DB}{BC}\)
Nên: \(\frac{AD}{AC}=\frac{DB}{BC}=\frac{AD+DB}{AC+BC}=\frac{AB}{AC+BC}\)
Hay: \(\frac{AD}{4}=\frac{DB}{5}=\frac{3}{4+5}=\frac{1}{3}\)
⇒ \(AD=\frac{4}{3}\left(cm\right)\)
\(DB=\frac{5}{3}\left(cm\right)\)
Cho hình chữ nhật ABCD. Vẽ AH vuông góc BD (H\(\in\)BD), HK//CD (K\(\in\)BC).
a) CM: tam giác ADH đồng dạng với tam giác DBC
b) CM: CD.BK=AH.BH
c) Cho biết AB=5cm, HB=4cm. Tính BK?

Lời giải:
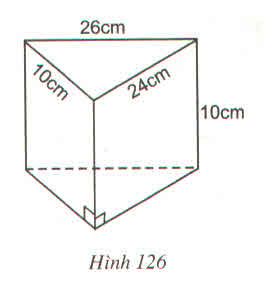
a) Diện tích tam giác đều cạnh $a$ bằng: \(\frac{\sqrt{3}a^2}{4}\). Áp dụng vào bài:
\(S_{\text{đáy}}=S_{ABC}=\frac{\sqrt{3}.6^2}{4}=9\sqrt{3}\) (cm2)
Với $h$ là chiều cao:
\(V=S_{\text{đáy}}.h\Leftrightarrow 90\sqrt{3}=9\sqrt{3}.h\Rightarrow h=10\) (cm)
b) Do đây là lăng trụ đứng nên các cạnh bên đều là hình chữ nhật và vuông góc với đáy
$\Rightarrow ABB'A'$ là hình chữ nhật và $BB'=h$
$S_{ABB'A'}=AB.BB'=AB.h=6.10=60$ (cm2)
a, - Từ định lý hero ta có :
Sđáy lăng trụ = SABC = \(AB^2\frac{\sqrt{3}}{4}=6^2\frac{\sqrt{3}}{4}=9\sqrt{3}\left(cm^2\right)\)
- Ta lại có : Vlăng trụ = SABC .h = \(9\sqrt{3}.h=90\sqrt{3}\)
=> \(h=10\left(cm\right)\)
b, - Diện tích mặt bên ABB,A, là : \(AB.h=6.10=60\left(cm^2\right)\)

1/ Nếu x≤yx≤y và a<0a<0 thì:
A. ax≤ayax≤ay
B. ax≥ayax≥ay
C. ax<ayax<ay
D. ax>ayax>ay
CChọn đáp án B
2/Tập nghiệm của phương trình |−2x|=4|−2x|=4 là:
A. {2}{2}
B. {−2}{−2}
C. {−2;2}{−2;2}
D. {1;2}{1;2}
Chọn đáp án C
3/Một lăng trụ đứng có đáy là tam giác thì lăng trụ đó có bao nhiêu mặt:
A. 33
B. 44
C. 55
D. 66
Chọn đáp án C
4/Cho tam giác ABC có AD là phân giác của BÂC (D∈BC)(D∈BC), AB=3 cm, AC=6 cm, BD=4 cm.Khi đó độ dài cạnh DC bằng:
A. 2cm
B. 4cm
C. 6cm
D. 8cm
Chọn đáp án B
5/Cho ΔABCΔABC và MN//BCMN//BC (M∈AB,N∈AC)(M∈AB,N∈AC). Câu nào sau đây đúng:
A. MAAB=NCACMAAB=NCAC
B. MAMB=MNBCMAMB=MNBC
C. MAMB=NANCMAMB=NANC
D. NANC=MNBC
Chọn đáp án C
Ta có tam giác ABC vuông tại A