Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

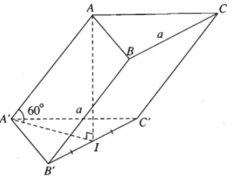
a) Gọi I là trung điểm của cạnh B'C'. Theo giả thiết ta có AI ⊥ (A'B'C') và ∠ A A ′ I = 60 ο . Ta biết rằng hai mặt phẳng (ABC) và (A'B'C') song song với nhau nên khoảng cách giữa hai mặt phẳng chính là khoảng cách AI.
Do đó
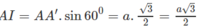
b) 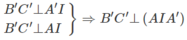
⇒ B′C′ ⊥ AA′
Mà AA′ // BB′ // CC′ nên B’C’ ⊥ BB’
Vậy mặt bên BCC’B’ là một hình vuông vì nó là hình thoi có một góc vuông.

a: Các mặt bên của hình lăng trụ này vừa là hình chữ nhật, vừa vuông góc với đáy
b: Các mặt bên của hình lăng trụ này vừa là hình chữ nhật, vừa vuông góc với đáy
c: Có 4 mặt bên là hình chữ nhật
d: Có tất cả là 6 mặt là hình chữ nhật

a) Trong hình chóp S.MNP, các thành phần được kể tên như sau:
Đỉnh: SCác cạnh bên: SM, SN, SPCạnh đáy: MNPMặt bên: Các mặt tam giác SMN, SNP, SMPMặt đáy: Tam giác MNPb) Để tìm giao tuyến của hai mặt phẳng (SMN) và (MNP), chúng ta cần tìm đường thẳng giao của hai mặt phẳng này. Đường thẳng này chính là đường thẳng chứa đường chéo của tam giác MNP, vì đường chéo của tam giác nằm trên mặt phẳng (SMN) và (MNP) cùng một lúc.
c) Để tìm giao tuyến của hai mặt phẳng (SMP) và (SNP), chúng ta cũng cần tìm đường thẳng giao của hai mặt phẳng này. Đường thẳng này chính là đường thẳng chứa cạnh SP của tam giác SNP và cạnh SP của tam giác SMP, vì cả hai cạnh này nằm trên mặt phẳng (SMP) và (SNP) cùng một lúc.

a: Đỉnh: S
Cạnh bên: SM,SN,SP
Cạnh đáy: MN,MP,NP
Mặt bên: SNP,SMP,SNM
Mặt đáy: MNP
b: \(MN\subset\left(SMN\right)\)
\(MN\subset\left(MNP\right)\)
Do đó: \(\left(SMN\right)\cap\left(MNP\right)=MN\)
c: \(SP\subset\left(SMP\right)\)
\(SP\subset\left(SNP\right)\)
Do đó: \(\left(SMP\right)\cap\left(SNP\right)=SP\)

Một)- Đỉnh của hình chóp S.MNPQ là điểm S.- Các cạnh bên của hình chóp là SM, SN, NP, NQ, PQ.- Cạnh đáy của hình chóp là đoạn thẳng MN, NP, PQ và QM.- Mặt bên của hình chóp là tam giác SMN, SNP, NQP và QMS.- Mặt đáy của hình chóp là hình chữ nhật MNPQ.b) Giao tuyến của hai mặt phẳng (SPQ) và (MNPQ) là một đường thẳng. Gọi đường thẳng này là d.c) Giao tuyến của hai mặt phẳng (SMQ) và (SQP) cũng là một đường thẳng. Gọi đường thẳng này là e.



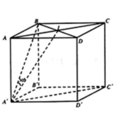





Mặt đáy: (ABCD),(A'B'C'D')
Đỉnh: A,B,C,D,A',B',C',D'
Cạnh bên: AA',BB',CC',DD'
Mặt bên: (AA'D'D), (BB'C'C), (ABB'A')
Cạnh đáy: AB,BC,CD,DA,A'B',B'C',C'D',D'A'