Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

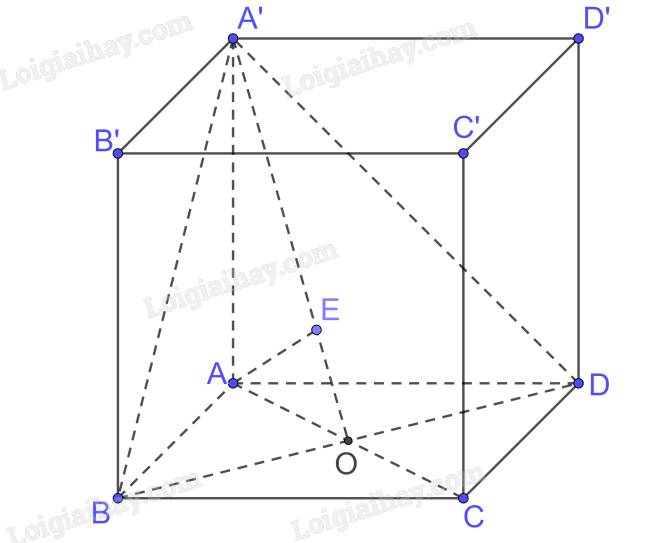
a) Diện tích tam giác ABD bằng diện tích tam giác BCD vì chung đáy BD và chiều cao AO = OC (ABCD là hình thoi)
Diện tích tam giác ABD: \({S_{ABD}} = \frac{1}{2}AB.AD.\sin \widehat {BAD} = \frac{1}{2}a.a.\sin {60^0} = \frac{{{a^2}\sqrt 3 }}{4}\)
\( \Rightarrow S = 2{S_{ABD}} = \frac{{{a^2}\sqrt 3 }}{2}\)
Thể tích khối hộp là \(V = AA'.{S_{ABCD}} = a.\frac{{{a^2}\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{2}\)
b) Gọi \(AC \cap BD = \left\{ O \right\}\)
Ta có \(AA' \bot BD,AO \bot BD \Rightarrow BD \bot \left( {A'AO} \right);BD \subset \left( {A'BD} \right) \Rightarrow \left( {A'AO} \right) \bot \left( {A'BD} \right)\)
\(\left( {A'AO} \right) \cap \left( {A'BD} \right) = A'O\)
Trong (A’AO) kẻ \(AE \bot A'O\)
\( \Rightarrow AE \bot \left( {A'BD} \right) \Rightarrow d\left( {A,\left( {A'BD} \right)} \right) = AE\)
Xét tam giác ABD có AB = AD và \(\widehat {BAD} = {60^0}\) nên tam giác ABD đều
\( \Rightarrow OA = \frac{{a\sqrt 3 }}{2}\)
Xét tam giác AOA’ vuông tại A có
\(\frac{1}{{A{E^2}}} = \frac{1}{{A{{A'}^2}}} + \frac{1}{{O{A^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}} = \frac{7}{{3{a^2}}} \Rightarrow AE = \frac{{a\sqrt {21} }}{7}\)
Vậy \(d\left( {A,\left( {A'BD} \right)} \right) = \frac{{a\sqrt {21} }}{7}\)

ta có :
\(V_{M.AB'C}=V_{B'.MAC}=\frac{B'B.S_{ABC}}{3}\)
Mà BB'=A'A=a
\(S_{AMC}=\frac{CD.AM}{2}=\frac{a.2a}{2.3}=\frac{a^2}{3}\)
=> \(V_{M.AB'C}=\frac{a^3}{9}\) (1)
=> dM,(AB'C)=\(\frac{3.V_{M.AB'C}}{S_{AB'C}}\) (2)
tam giác AB'C cps \(AB=B'C=2\sqrt{3}\)
và \(AB=a\sqrt{2}\)
=>\(S_{AB'C}=\frac{a^2\sqrt{5}}{2}\) (3)
Từ (1), (2)&(3)
=> dM;(AB'C)=\(\frac{2a}{3\sqrt{a}}\)
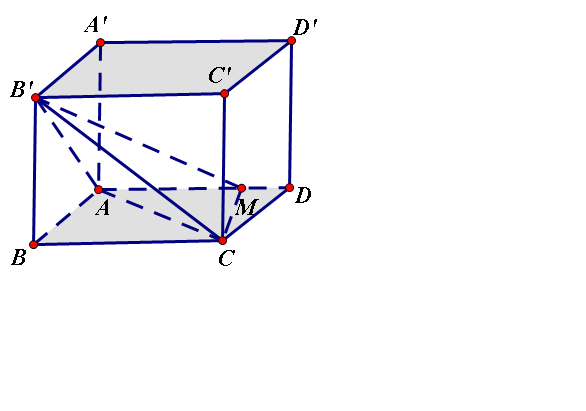
Pytago tính đuợc 3 cạnh ΔAMC
\(AC=a\sqrt{5}\); \(AM=\frac{3a}{2}\), \(MC=\frac{a\sqrt{5}}{2}\)
Dùng công thức HeronHeron =>\(S_{AMC}=\frac{3a^2}{4}\)
\(V_{M.AB'C}=V_{B.AB'C}=\frac{a^3}{4}\)
Mặt khác dùng công thức HeronHeron cũng tính được \(S_{AB'C}=\frac{3a^2}{2}\)
=> \(d_{\left(M;\left(AB'C\right)\right)}=\frac{3V_{M.AB'C}}{S_{AB'C}}=\frac{a}{2}\)

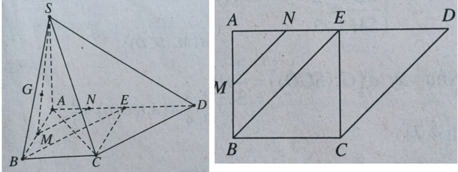
+ Xác định góc của SC với (SAD).
Hạ CE ⊥ AD, ta có E là trung điểm AD và CE ⊥ (SAD) nên ∠(CSE) = 30 o .
∠(CSE) cũng chính là góc giữa SC và mp(SAD).
Trong ΔCSE, ta có:
S E = C E . tan 60 o = a 3 ⇒ S A = S E 2 - A E 2 = 3 a 2 - a 2 = a 2 .
Nhận xét
Gọi M, N lần lượt là trung điểm của AB và AE.
Ta có MN // BE nên MN // CD. Như vậy MN // (SCD). Ta suy ra
d(M,(SCD)) = d(N,(SCD)).
Mà DN/DA = 3/4 nên d(N,(SCD)) = 3/4 d(A,(SCD))
+ Xác định khoảng cách từ A đến (SCD).
Vì vậy tam giác ACD vuông cân tại C nên CD vuông góc với AC.
CD ⊥ AC & CD ⊥ SA ⇒ CD ⊥ (SAC) ⇒ (SCD) ⊥ (SAC).
Hạ AH ⊥ SC, ta có AH ⊥ (SCD).

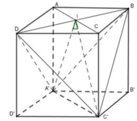


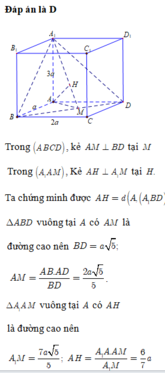

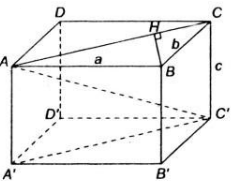

Gọi O là giao điểm AC và BD \(\Rightarrow O\) là trung điểm BD và AC
Do G là trọng tâm tam giac BCD \(\Rightarrow OG=\dfrac{1}{3}OC=\dfrac{1}{3}OA\)
Mà \(GA\cap\left(A'BD\right)=O\Rightarrow d\left(G;\left(A'BD\right)\right)=\dfrac{1}{3}d\left(A;\left(A'BD\right)\right)\)
Trong mp (ABCD), từ A kẻ \(AH\perp BD\)
Trong mp (A'AH), từ A kẻ \(AK\perp A'H\)
\(\Rightarrow AK\perp\left(A'BD\right)\Rightarrow AK=d\left(A;\left(A'BD\right)\right)\)
Hệ thức lượng tam giác vuông ABD:
\(AH=\dfrac{AB.AD}{\sqrt{AB^2+AD^2}}=\dfrac{2a\sqrt{5}}{5}\)
Hệ thức lượng trong tam giác vuông A'AH:
\(AK=\dfrac{A'A.AH}{\sqrt{A'A^2+AH^2}}=\dfrac{2a}{3}\)
\(\Rightarrow d\left(G;\left(A'BD\right)\right)=\dfrac{1}{3}AK=\dfrac{2a}{9}\)