

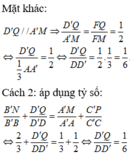
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



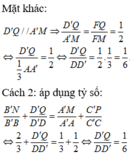

Đáp án A
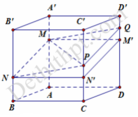
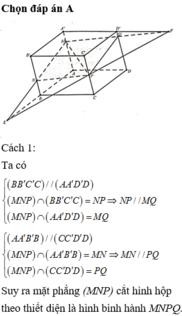
Lấy M’, N’ lần lượt trên các cạnh DD’ và CC’ sao cho M A = M ' D và N B = N ' C .
Vì A B B ' A ' / / C DD ' C ' nên 2 giao tuyến giữa mặt phẳng (MNP) lần lượt với các mặt phẳng (ABB'A') và (CDC'C') sẽ song song với nhau. Do vậy ta sẽ lấy Q ∈ DD ' sao cho M N / / P Q . Ta có:
D Q ' = D ' M ' − Q M ' = DD ' 3 − P C − N ' C = DD ' 3 − DD ' 2 − DD ' 3 = DD ' 6 ⇒ D ' Q DD ' = 1 6 .

Đáp án A
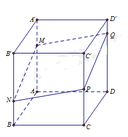
Ta chứng minh được công thức tỷ số thể tích tối với khối hộp như sau (học sinh có thể tự chứng minh).
V A ' B ' C ' D ' . M N P Q V A " B ' C ' D ' . A B C D = 1 2 A ' M A ' A + C ' P C ' C = 1 2 B ' N B ' B + D Q D ' D
Khi đó: 1 3 + 1 2 = 2 3 + D Q D ' D ⇔ D Q D ' D = 1 6 .

bài 1
\(A+B=a+b-5-b-c+1=a-c-4\)
\(A+B+C+D=a-c-4+b-c-4+b-a=2b-2c\)
\(A-B+C-D=a+b-5+b+c-1+b-c-4+a-b\)
\(A-B+C-D=2a+2b-10\)
\(A+B=a-c-4\)
\(C-D=b-c-4-b+a=a-c-4\)
\(A+B=C-D\)

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

Đáp án C
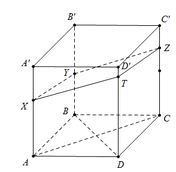
Ta có: V A ' B ' C ' D ' . X Y Z T V A ' B ' C ' D ' . A B C D = 1 2 A ' X A ' A + C ' Z C ' C = 1 2 . 1 3 + 1 4 = 7 24
Cho V X Y Z T . A ' B ' C ' D ' = 7 ; V A ' B ' C ' D ' . A B C D = 24
Khi đó V X Y Z T . A B C D = 17 ⇒ k = 17 7 .