Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

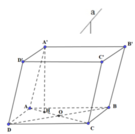
∆ A O D vuông tại O
⇒ O A = A D 2 - O D 2 = a 2 - 3 a 2 2 = a 2 ⇒ A H = 1 2 A O = a 4 ;
AC=2.AO=a và S A B C D = 1 2 . A C . B D
= 1 2 a . a . 3 = a 2 3 2
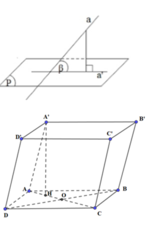
Do AA'//CC' nên
∠ ( A A ' ; ( A B C D ) ) = ∠ ( C C ' ; A B C D ) = 60 °
Do
A H ⊥ ( A B C D ) ⇒ ∠ ( A A ' ; ( A B C D ) ) = ∠ ( A A ' ; A H ) = ∠ A ' A H = 60 °
∆ A ' A H vuông tại
H ⇒ A ' H = A H . tan A ' A H = a 4 . tan 60 ° = a 3 4
Thể tích khối hộp là V = S A B C D . A ' H
= a 2 3 2 . a 3 4 = 3 a 3 8
Chọn đáp án A.

Đáp án D
Phương pháp:
Thể tích hình hộp trong đó:
B: diện tích đáy,
h: chiều cao
Cách giải:
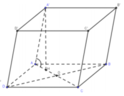
Do AA’ // CC’ nên (AA’,ABCD) = (CC’,ABCD) = 600
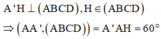
Hình thoi ABCD có AB = CD = BC = DA = a. BD= B'D' = a 3
Tam giác OAB vuông tại O:
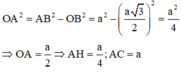
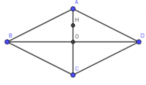
Diện tích hình thoi ABCD: 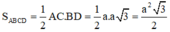
Tam giác A’AH vuông tại H:
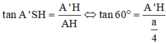
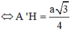
Thể tích hình hộp ABCD.A’B’C’D’:
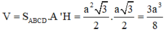

Theo công thức ta có:
Sxq = 2πrh = 2√3 πr2
Stp = 2πrh + 2πr2 = 2√3 πr2 + 2 πr2 = 2(√3 + 1)πr2 ( đơn vị thể tích)
b) Vtrụ = πR2h = √3 π r3
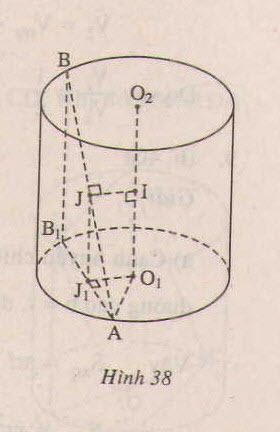
c) Giả sử trục của hình trụ là O1O2 và A nằm trên đường tròn tâm O1, B nằm trên đường tròn tâm O2; I là trung điểm của O1O2, J là trung điểm cảu AB. Khi đó IJ là đường vuông góc chung của O1O2 và AB. Hạ BB1 vuông góc với đáy, J1 là hình chiếu vuông góc của J xuống đáy.
Ta có là trung điểm của
,
= IJ.
Theo giả thiết = 300.
do vậy: AB1 = BB1.tan 300 = = r.
Xét tam giác vuông
AB1 = BB1.tan 300 = O1J1A vuông tại J1, ta có: =
-
.
Vậy khoảng cách giữa AB và O1O2 :

Đáp án D
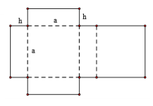
Thể tích khối hộp V = S h = h a 2
Diện tíc của tấm bìa là S b = 4 a h + 2 a 2 = 3 ⇔ h = 3 - 2 a 2 4 a 2
Từ 1 và 2 suy ra V = h a 2 = 3 - 2 a 2 4 a a 2 = a 3 - 2 a 2 4 ≤ 2 4 (khảo sát hàm số)
Dấu “=” xảy ra khi a = 1 2 ⇒ thế vào (2) ta được h = 2 2 ⇒ a + h = 2 .

Phương pháp:
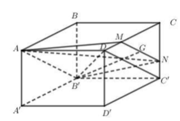
- Dựng mặt phẳng chứa B'G và song song với C'D.
- Xác định khối đa diện và tính thể tích bằng cách cộng trừ thể tích các khối đa diện đơn giản.
Cách giải:

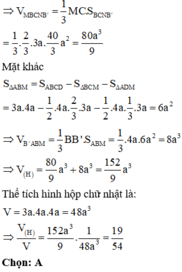




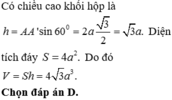
Đáp án A
Diện tích hình thoi ABCD là