Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

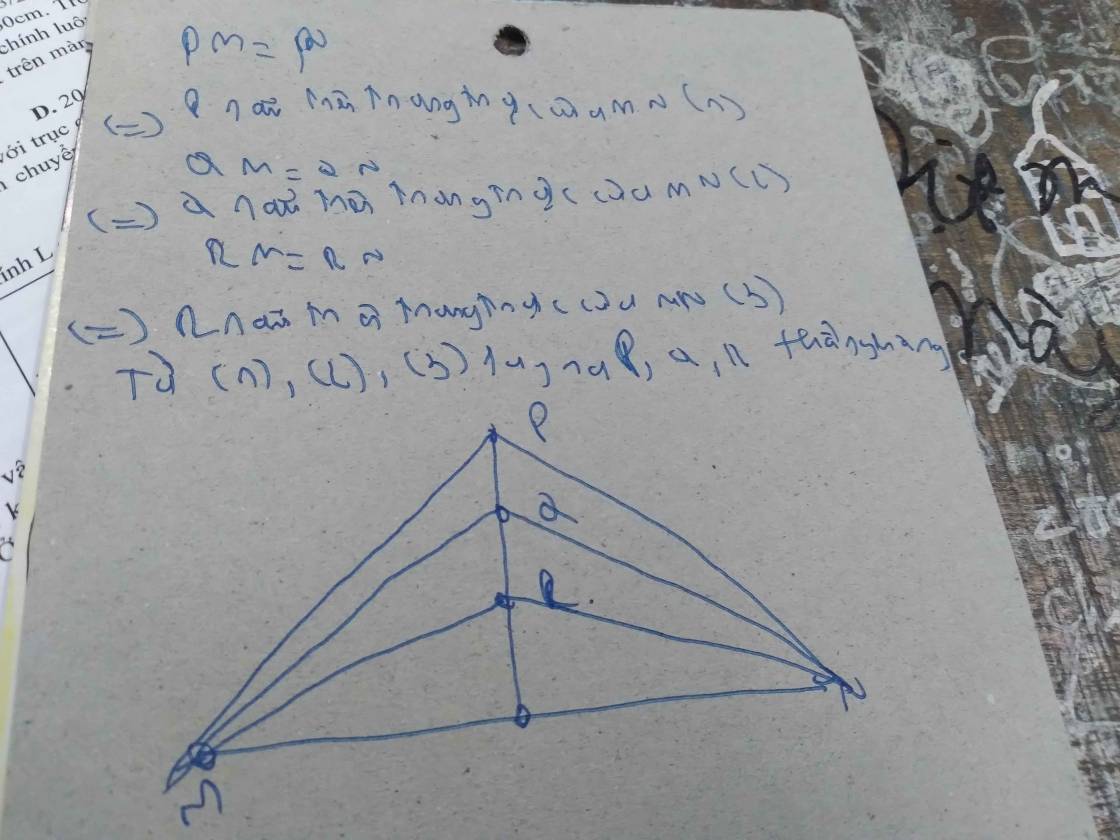
- Theo tính chất của đường trung trực : Mọi điểm cách đều hai mút của đoạn thẳng là đường trung trực .
=> Đường thẳng đi qua 3 điểm P, R, Q là đường trung trực của MN .
=> Ba điểm P, R, Q thẳng hàng .

Ta có hình vẽ sau:
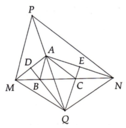
M P Q N I A R
a/ Xét ΔAMQ và ΔANP có:
AM = AN (gt)
\(\widehat{MAQ}=\widehat{NAP}\) (đối đỉnh)
AQ = AP (gt)
=> ΔAMQ = ΔANP (c.g.c) (đpcm)
b/ Vì ΔAMQ = ANP (ý a)
=> \(\widehat{QMA}=\widehat{PNA}\) (2 góc tương ứng)
mà 2 góc này lại ở vị trí so le trong nên
=> MQ // PN (đpcm)
c/+) Xét ΔAMI và ΔANR có:
\(\widehat{MAI}=\widehat{NAR}\) (đối đỉnh)
AM = AN(gt)
\(\widehat{AMI}=\widehat{RNA}\) (so le trong do MQ // PN (ý b))
=> ΔAMI = ΔANR (g.c.g)
=> MI = NR (1)
+) CM tương tự ta có:
ΔAQI = ΔAPR (g.c.g)
=> QI = PR (2)
Từ (1); (2) và I là trung điểm của MQ
=> RP = RN (đpcm)

1) Ta có \(M=\left|x+1\right|+\left|2x-10\right|+\left|2x-7\right|+\left|x-\frac{11}{2}\right|\)
\(=\left|x+1\right|+\left|\frac{11}{2}-x\right|+\left|2x-10\right|+\left|7-2x\right|\)
\(\ge\left|\frac{13}{2}\right|+\left|-3\right|=\frac{19}{2}\)
Dấu bằng xảy ra khi \(\hept{\begin{cases}\left(x+1\right)\left(\frac{11}{2}-x\right)\ge0\\\left(2x-10\right)\left(7-2x\right)\ge0\end{cases}}\Leftrightarrow\frac{7}{2}\le x\le5\)

PMNIEFKH
a) Xét \(\Delta PIM;\Delta PIN\) có :
\(PM=PN\) (tam giác MNP cân tại P)
\(\widehat{MPI}=\widehat{NPI}\) (PI là tia phân giác của \(\widehat{MPN}\) )
\(PI:chung\)
=> \(\Delta PIM=\Delta PIN\left(c.g.c\right)\)
*Cách khác :
Xét \(\Delta PIM;\Delta PIN\) có :
\(\widehat{PMI}=\widehat{PNI}\) (tam giác MNP cân tại P)
\(PM=PN\)(tam giác MNP cân tại P)
\(\widehat{MPI}=\widehat{NPI}\) (PI là tia phân giác của góc MPN)
=> \(\Delta PIM=\Delta PIN\left(g.c.g\right)\)
b) Xét \(\Delta PEI;\Delta PFI\) có :
\(\widehat{PEI}=\widehat{PFI}\left(=90^{^O}\right)\)
\(PI:Chung\)
\(\widehat{EPI}=\widehat{FPI}\left(cmt\right)\)
=> \(\Delta PEI=\Delta PFI\) (cạnh huyền - góc nhọn)
=> \(IE=IF\) (2 cạnh tương ứng)
c) Ta chứng minh được \(\Delta PIK=\Delta PIH\left(g.c.g\right)\)
Suy ra : \(PK=PH\) (2 cạnh tương ứng)
Xét \(\Delta PHK\) có :
\(PK=PH\left(cmt\right)\)
=> \(\Delta PHK\) cân tại P (đpcm)
d) Xét \(\Delta PEF\) cân tại E có :
\(\widehat{PEF}=\widehat{PFE}=\dfrac{180^o-\widehat{P}}{2}\left(1\right)\)
Xét \(\Delta PKH\) cân tại P (cmt) có :
\(\widehat{PKH}=\widehat{PHK}=\dfrac{180^o-\widehat{P}}{2}\left(2\right)\)
Từ (1) và (2) => \(\widehat{PEF}=\widehat{PKH}\left(=\dfrac{180^o-\widehat{P}}{2}\right)\)
Mà thấy : 2 góc này đều ở vị trí đồng vị
=> \(\text{EF // HK (đpcm)}\)