Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a. Vì $ABCD$ là hình chữ nhật nên $\widehat{A}=\widehat{D}=90^0$
$MN\perp CD$ nên $\widehat{MND}=90^0$
Tứ giác $AMND$ có 3 góc vuông $\widehat{A}=\widehat{D}=\widehat{N}$ nên là hcn.
b.
Hoàn toàn tương tự phần a ta thấy $\widheat{B}=\widehat{C}=\widehat{N}$ nên $BMNC$ là hcn
$\Rightarrow BM=NC$
$AMND$ là hcn nên $AM=DN$
Mà $AM=BM$ nên $AM=NC$
Có $AM\parallel NC$ (do $AB\parallel CD$) và $AM=NC$ nên $AMCN$ là hbh
$\Rightarrow AC, MN$ cắt nhau tại trung điểm mỗi đường.
Mà $O$ là trung điểm $MN$ nên $O$ cũng là trung điểm $AC$.
c.
Vì $AMCN$ là hbh (theo phần b) nên $AN\parallel CM$
$\Rightarrow EN\parallel FC$
$\Rightarrow \frac{DE}{EF}=\frac{DN}{NC}=1$ (theo định lý Talet)
$\Rightarrow DE=EF(1)$
Mặt khác:
$AN\parallel CM$
$\Rightarrow MF\parallel AE$
$\Rightarrow \frac{BF}{EF}=\frac{BM}{MA}=1$ (định lý Talet)
$\Rightarrow BF=EF(2)$
Từ $(1); (2)\Rightarrow DE=EF=BF$

A B C D M N O
Xét tứ giác AMND có góc \(A=D=M=90^0\), do đó AMND là hình chữ nhật.
do AMND là hình chữ nhật nên \(AM=ND=NC\) mà AM//NC
do đó AMCN là hình bình hành
do đó AC cắt MN tại trung điểm của mỗi đường, do đó ta có đpcm

a: Xét tứ giác AMND có
\(\widehat{ANM}=\widehat{MAD}=\widehat{ADN}=90^0\)
=>AMND là hình chữ nhật
b: AMND là hình chữ nhật
=>AM=ND
mà \(AM=\dfrac{AB}{2}\) và AB=CD
nên DN=DC/2
=>N là trung điểm của CD
AM=MB=AB/2
CN=ND=CD/2
mà AB=CD
nên AM=MB=CN=ND
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
=>AC cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của MN
nên O là trung điểm của AC

a: Xét tứ giác AMND có
\(\widehat{MAD}=\widehat{ADN}=\widehat{MND}=90^0\)
nên AMND là hình chữ nhật

1: Xét tứ giác AMND có
\(\widehat{ADN}=\widehat{DAM}=\widehat{MND}=90^0\)
Do đó: AMND là hình chữ nhật
2: Xét tứ giác AKBD có
M là trung điểm của đường chéo KD
M là trung điểm của đường chéo AB
Do đó: AKBD là hình bình hành
Trả lời:
1: Xét tứ giác AMND có
ˆADN=ˆDAM=ˆMND=900ADN^=DAM^=MND^=900
Do đó: AMND là hình chữ nhật
2: Xét tứ giác AKBD có
M là trung điểm của đường chéo KD
M là trung điểm của đường chéo AB
Do đó: AKBD là hình bình hành
Chúc bạn học tốt nhé.

a: Xét tứ giác ANMP có
\(\widehat{ANM}=\widehat{APM}=\widehat{PAN}=90^0\)
Do đó: ANMP là hình chữ nhật

Có vẻ đề của bạn bị sai *_*. Mình có làm đề này rồi nên mình chỉ sửa đề của bạn 1 chút là''Gọi H là chân đường vuông góc kẻ từ điểm A đến BC'' thế thôi, còn lại là đúng. Bây giờ mình sẽ giải cho bạn.
A B C D H I M N
*Mình vẽ không đc đẹp, bạn thông cảm nha*
a/
Ta có, AM=HM và HN=DN(gt)
-> MN là đường trung bình của tam giác AHB
->MN//AD
b/
Ta có, MN // AD ( câu a/) ; AD // AB (tính chất của hình chữ nhật)
-> MN // BI(I nằm trên cạn BC) (1)
Lại có: MN = 1/2 AD(MN là đường trung bình của tam giác AHB)
Mà BI= 1/2 BC và BC=AD
->MN=BI (2)
Từ (1) và (2) -> Tứ giác BMNI là hình bình hành
c/
Vì AH vuông góc với BD(gt) VÀ MN vuông góc với AB(vì MN // AD ; AD vuông góc với AB)
-> M là trực tâm của tam giác ABN
Mà BM // IN
-> AN vuông góc với IN
hay góc ANI= 90 độ
-> Tam giác ANI vuông tại N(đpcm)
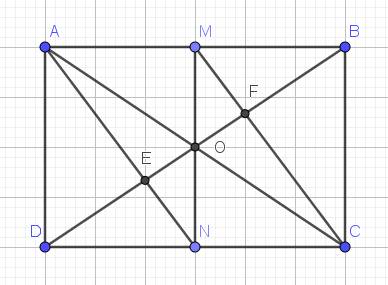
a: Xét tứ giác AMND có
\(\widehat{MND}=\widehat{ADN}=\widehat{DAM}=90^0\)
=>AMND là hình chữ nhật
b: AMND là hình chữ nhật
=>AM=ND
mà \(AM=\dfrac{AB}{2}\)
nên \(ND=\dfrac{AB}{2}\)
mà AB=CD(ABCD là hình chữ nhật)
nên \(ND=\dfrac{CD}{2}\)
=>N là trung điểm của CD
=>NC=ND
AM=ND
ND=NC
Do đó: AM=NC
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
=>AC cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của MN
nên O là trung điểm của AC