Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABD có
H,O lần lượt là trung điểm của BA,BC
=>HO là đường trung bình của ΔABD
=>HO//AD và \(HO=\dfrac{AD}{2}\)
\(HO=\dfrac{AD}{2}\)
\(AK=\dfrac{AD}{2}\)
Do đó: HO=AK
Xét tứ giác AHOK có
HO//AK
HO=AK
Do đó: AHOK là hình bình hành
Hình bình hành AHOK có \(\widehat{HAK}=90^0\)
nên AHOK là hình chữ nhật
Gọi N là giao điểm của AO và HK
AHOK là hình chữ nhật
=>AO=HK và AO cắt HK tại trung điểm của mỗi đường
=>AO=HK và N là trung điểm chung của AO và HK
=>\(AN=ON=HN=KN=\dfrac{AO}{2}=\dfrac{HK}{2}\left(1\right)\)
ΔAMO vuông tại M
mà MN là đường trung tuyến
nên \(MN=\dfrac{AO}{2}\left(2\right)\)
Từ (1),(2) suy ra \(MN=\dfrac{HK}{2}\)
Xét ΔKMH có
MN là đường trung tuyến
\(MN=\dfrac{HK}{2}\)
Do đó: ΔKMH vuông tại M
=>KM\(\perp\)MH tại M

Tứ giác có thể là hình vuông, chữ nhật phải không bạn?
P/s: Hỏi thôi chớ không trả lời đâu :D

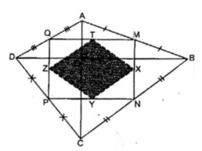
Trong △ ABD ta có:
M là trung điểm của AB
Q là trung điểm của AD nên MQ là đường trung bình của △ ABD.
⇒ MQ // BD và MQ = 1/2 BD (tính chất đường trung bình của tam giác) (1)
Trong △ CBD ta có:
N là trung điểm của BC
P là trung điểm của CD
nên NP là đường trung bình của △ CBD
⇒ NP // BD và NP = 1/2 BD (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: MQ // NP và MQ = NP nên tứ giác MNPQ là hình bình hành
AC ⊥ BD (gt)
MQ // BD
Suy ra: AC ⊥ MQ
Trong △ ABC có MN là đường trung bình ⇒ MN // AC
Suy ra: MN ⊥ MQ hay (NMQ) = 90 0
Vậy tứ giác MNPQ là hình chữ nhật.

Em tham khảo tại đây nhé:
Câu hỏi của Nguyễn Chí Thành - Toán lớp 8 - Học toán với OnlineMath
ai thương em thì làm ny em nha trên 12 tủi
Lời giải ở đây: https://sites.google.com/site/123onthi/toan8