Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đầu bài chỗ " đường chéo BD cắt AE" chắc là " đường chéo BD cắt AI" phải không bn???
a) ta có: AB = CD ( ABCD là h.b.h)
=> AK = IC \(\left(=\frac{1}{2}AB=\frac{1}{2}CD\right)\)
mà AK // IC
=> AKCI là hình bình hành ( dấu hiệu)
xét \(\Delta DFC\)
có: DI =IC (gt)
EI // FC ( AKCI là h.b.h)
=> EI là đường trung bình của \(\Delta DFC\)
=> DE = EF ( t/c')
cmtt với \(\Delta AEB\)ta có: EF = FB
=> DE=EF=FB
b) xét \(\Delta ABD\)
có: AM=MD
AK=KB
=> KM là đường trung bình của \(\Delta ABD\)
=> KM // BD và \(KM=\frac{1}{2}BD\)
cmtt với \(\Delta BCD\)ta có: IN//BD và \(IN=\frac{1}{2}BD\)
=> KM // IN (//BD)
\(KM=IN\left(=\frac{1}{2}BD\right)\)
=> KMIN là hình bình hành ( dấu hiệu)

a) Xét tam giác ABD có :
M là trung điểm của AB
F là trung điểm của BD
=) MF là đường trung bình của tam giác ABD
=) MF//AD và MF=\(\frac{1}{2}\)AD (1)
Xét tam giác tam giác ACD có :
N là trung điểm CD
E là trung điểm AC
=) NE là đường trung bình của tam giác ACD
=) NE//AD và NE=\(\frac{1}{2}\)AD (2)
Từ (1) và (2) =) Tứ giác MENF là hình bình hành

a) Xét ∆ABC có :
D là trung điểm AB
E là trung điểm BC
=> DE là đường trung bình ∆ABC
=> DE//AC , DE = \(\frac{1}{2}AC\)= \(\frac{16}{2}=8\)cm
Xét ∆ABC có :
E là trung điểm BC
F là trung điểm AC
=> FE là đường trung bình ∆ABC
=> FE//AB , FE = \(\frac{1}{2}AB=6cM\)
Xét tứ giác AFED có :
AD//EF ( AB//FE , D\(\in\)AB )
DE//FA ( DE//AC , F \(\in\)AC )
=> AFED là hình bình hành
Mà BAC = 90°
=> AFED là hình chữ nhật
=> DEF= EFA = FAD = ADE = 90°
Vì F là trung điểm AC
=> FA = FC = 8cm
Áp dụng định lý Py - ta -go vào ∆AEF ta có :
AE2 = FE2 + AF2
=> AE = 10cm
b) Xét ∆ABC ta có :
D là trung điểm AB
F là trung điểm AC
=> DF là đường trung bình ∆ABC
=> DF//BC
Xét tứ giác BEFD ta có :
BE//DF ( BC//DF , E \(\in\)BC )
BD//FE ( AB//FE , D\(\in\)AB )
=> BEFD là hình bình hành
c) Chứng minh trên

a) Ta chứng minh A N = C M A N ∥ C M ⇒ A M C N là hình bình hành.
Vì O là giao điểm của AC và BD, ABCD là hình chữ nhật nên O là trung điểm AC
Do ANCM là hình bình hành có AC và MN là hai đường chéo
⇒ O là trung điểm MN
b. Ta có: EM//AC nên E M D ^ = A C D ^ (2 góc so le trong)
NF//AC nên B N F ^ = B A C ^ (2 góc so le trong)
Mà A C D ^ = B A C ^ (vì AB//DC, tính chất hình chữ nhật)
⇒ E M D ^ = B N F ^
Từ đó chứng minh được ∆ E D M = ∆ F B N ( g . c . g )
⇒ E M = F N
Lại có EM//FN (vì cùng song song với AC)
Nên tứ giác ENFM là hình bình hành
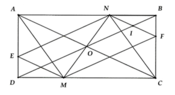
c) Tứ giác ANCM là hình thoi Û AC ^ MN tại O Þ M, N lần lượt là giao điểm của đường thẳng đi qua O, vuông góc AC và cắt CD, AB.
Khi đó M và N là trung điểm của CD và AB.
d) Ta chứng minh được DBOC cân tại O ⇒ O C B ^ = O B C ^ v à N F B ^ = O C F ^ (đv) Þ DBFI cân tại I Þ IB = IF (1)
Ta lại chứng minh được DNIB cân tại I Þ IN = IB (2)
Từ (1) và (2) Þ I là trung điểm của NF.

Bài 2 :
A B C D M E
a, Xét tam giác ABC ta có :
D là trung điểm AB
M là trung điểm CB
=)) DM là đường TB tam giác ABC
=)) DM // AC hay DM // AE (1)
Ta có : E là trung điểm AC
M là trung điểm BA
=)) EM là đường TB tam giác ABC
=)) EM // AB hay EM // AD (2)
Từ 1;2 =)) Tứ giác ADME là hình bình hành
b, Nếu tam giác ABC cân tại A => AM là đường trung tuyến AM
=)) AM đồng thời là tia phân giác của ^A
Xét hình bình hành ADME có 2 đường chéo AM là tia phân giác của ^A (cmt)
=)) Tứ giác ADME là hình thoi
c, Nếu tam giác ABC vuông tại A => ^A = 90^0
Xét hình bình hành ADME có ^A =90^0
=)) Tứ giác ADME là hình chữ nhật

2/
a/ hình thang ABCD có
AB // EF
==> AB // KF
xét tam giác ABC có
F là trung điểm của BC
AB // KF
==> KF là đường trung bình của tam giác ABC
==> K là trung điểm của AC
==> AK = KC
b/
E là trung điểm AD
F là trung điểm BC
==> EF là đường trung bình của hình thang ABCD
==> EF = (AB + CD) / 2 = (4 + 10) / 2 = 7(cm)
KF là đường trung bình của tam giác ABC nên
KF = AB / 2 = 4 / 2 = 2(cm)
==> EK = EF - KF = 7 - 2 = 5(cm)
vậy EK = 5(cm), KF = 2 (cm)
3/
a/ ta có
D là trung điểm của AB
M là trung điểm của BC
==> DM là đường trung bình của tam giác ABC
==> Dm // AC
==> DM // AE ( E thuộc AC, DM // AC)
chứng minh tương tự ta có
ME là đường trung bình của tam giác ABC
==> AD // ME
tứ giác ADME có DM // AE, AD // ME nên là HBH
b/ ( nếu tam giác ABC cân tại A)
tam giác ABC cân tại A ==> AB = AC
AD = 1/2 AB (D là trung điểm của AB)
AE = 1/2 AC (E là trung điểm của AC)
==> AD = AE
c/ (nếu tam giác ABC vuông)
ta có
tứ giác ADME là HBH
góc A = 90 độ
==> tứ giác ADME là HCN
d/ ta có
AB^2 + AC^2 = BC^2
6^2 + 8^2 = 100
==> BC = 10(cm)
AM là đường trung tuyến của tam giác ABC
==> AM = 1/2 BC = 1/2 . 10 = 5(cm)
vậy AM = 5cm
Bài 2:Cho mk ý kiến,sai đề à???4cm=6cm nhé

Bài 3:

Bài 4:
Nối D với E, nối D với M:
Chứng minh được ED//FB (BEDF là hình thoi) (1)
BF là đường trung bình tam giác AMD
=> MD//FB (tc) (2)
(1),(2) => MD trùng với ED (định lý) ( Qua 1 điểm ko thuộc đường thẳng a có 1 và chỉ 1 đường thẳng đi qua điểm đó và song song với đường thẳng a )
từ đó bạn có thể cm BMCD là hình chữ nhật ( nếu cần )
( xét từ1 giác BDCM có BC cắt DM tại trung điểm của mỗi đoạn ->BMCD là Hình chữ nhật)
Bài 5:

a: Xét tứ giác ANCM có
AM//CN
AM=CN
Do đó: ANCM là hình bình hành