Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E F
Giải
Kẻ EF \(\perp\) CD (F \(\in\) CD), dễ thấy các tứ giác BCFE và AEFD cũng là các hình chữ nhật (vì ABCD là hình chữ nhật)
\(\Rightarrow\) BC = EF = AD ; AE = DF ; EB = CF
\(\left\{\begin{matrix}\Delta ADE=\Delta FED\left(c.c.c\right)\\\Delta BEC=\Delta FCE\left(c.c.c\right)\end{matrix}\right.\)\(\Rightarrow\left\{\begin{matrix}S_{ADE}=S_{FED}\\S_{BEC}=S_{FCE}\end{matrix}\right.\) \(\Rightarrow\left\{\begin{matrix}S_{AEFD}=2S_{FED}\\S_{BECF}=2S_{FCE}\end{matrix}\right.\)
\(\Rightarrow\) SAEFD + SBCFE = 2(SFED + SFCE) = 2SEDC
Do hai hình chữ nhật AEFD và BCFE không có điểm trong chung nên: SAEFD + SBCFE = SABCD
Vậy SABCD = SEDC

A B C D E H
Kẻ đường cao EH của ΔEDC
\(\Rightarrow EH=BC\)
\(S_{\Delta EDC}=\dfrac{1}{2}CD.EH\)
\(S_{ABCD}=CD.BC\)
Mà EH = BC
\(\Rightarrow S_{ABCD}=CD.EH\)
\(\dfrac{S_{ABCD}}{S_{\Delta EDC}}=\dfrac{CD.EH}{\dfrac{1}{2}CD.EH}=2\)
\(\Rightarrow S_{ABCD}=2S_{\Delta EDC}\)
Kẻ đường cao EH của tam giác EDC
\(\Rightarrow EH=BC\)
\(S\Delta EDC=\dfrac{1}{2}CD\times EH\)
Diện tích ABCD \(=CD\times BC\)
Mà EH \(=BC\)
\(\Rightarrow\)Diện tích ABCD \(=\)CD\(\times\)EH\(\dfrac{SABCD}{S\Delta EDC}=\dfrac{CD\times EH}{\dfrac{1}{2}CD\times EH}\)\(=\)2
\(\Rightarrow\)Diện tích ABCD\(=\)2S\(\Delta\)EDC

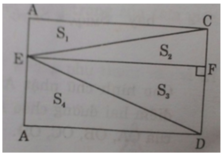
Kẻ EF ⊥ CD ⇒ AC // EF // AD
Xét ΔBCE và ΔFEC có:
(CAE) = (CFE) = 90o
(BCE) = (CEF) (Hai góc so le trong)
CE chung
⇒ ΔBCE = ΔFEC (cạnh huyền- góc nhọn)
tương tự ΔAED=ΔFDE.
Do đó (theo hình vẽ):
S1 = S2 và S3 = S4
⇒ S2 + S3 = S1 + S4 = (1/2)SABCD
Hay SECD = (1/2)SABCD ⇒ SABCD = 2SECD.

sai đầu bài rồi nhé. Cái này là vô lý. xem lại đầu bài nhé
đề sai rồi, mk không chứng minh
xét theo hình vẽ thì có có thể bé hơn 3 đến 4 lần