Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
![]() => Đường thẳng AB có pt là: x- y – 5= 0.
=> Đường thẳng AB có pt là: x- y – 5= 0.
Gọi G(a;3a- 8) suy ra C( 3a- 5; 9a -19).
Ta có:

Vậy C( 1 ; -1) và C( -2 ; 10)

Vì hình bình hành ABCD có tâm I => I là trung điểm của AC và BC
Vì I là trung điểm AC
=> \(\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_C}{2}\\y_I=\dfrac{y_A+y_C}{2}\end{matrix}\right.\)
=> xA = -2; yA = 5 => A(-2; 5)
Tương tự ta có D(7; 1)

Câu 32:
Gọi M là giao điểm d1;d2 thì tọa độ M là nghiệm của hệ:
\(\left\{{}\begin{matrix}3x-5y+2=0\\5x-2y+4=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{16}{19};-\frac{2}{19}\right)\)
Do d song song d3 nên d nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình d:
\(2\left(x+\frac{16}{19}\right)-1\left(y+\frac{2}{19}\right)=0\Leftrightarrow2x-y+\frac{30}{19}=0\)
Câu 33:
\(\overrightarrow{BC}=\left(1;-2\right)\)
Do AH vuông góc BC nên AH nhận \(\left(1;-2\right)\) là 1 vtpt
Phương trình AH:
\(1\left(x+1\right)-2\left(y-2\right)=0\Leftrightarrow x-2y+5=0\)
Câu 34:
Tọa độ M là: \(M\left(\frac{3}{2};4\right)\)
\(\overrightarrow{CM}=\left(-\frac{3}{2};6\right)=-\frac{3}{2}\left(1;-4\right)\)
Phương trình tham số CM: \(\left\{{}\begin{matrix}x=3+t\\y=-2-4t\end{matrix}\right.\)
Câu 30:
\(\overrightarrow{AB}=\left(-2;0\right)=-2\left(1;0\right)\) nên đường thẳng AB nhận \(\left(1;0\right)\) là 1 vtcp
Phương trình AB: \(\left\{{}\begin{matrix}x=1+t\\y=-7\end{matrix}\right.\)
Cả 4 đáp án đều ko chính xác
Câu 31:
Gọi M là trung điểm AB \(\Rightarrow M\left(-1;1\right)\)
\(\overrightarrow{AB}=\left(-6;-4\right)=-2\left(3;2\right)\Rightarrow\) đường trung trực AB nhận \(\left(3;2\right)\) là 1vtpt
Phương trình:
\(3\left(x+1\right)+2\left(y-1\right)=0\Leftrightarrow3x+2y+1=0\)

Đáp án B
Gọi hình bình hành là ABCD và
d:x+ y-1 = 0, ∆: 3x – y+ 5= 0 .
Không làm mất tính tổng quát giả sử
![]()
Ta có : ![]() . Vì I(3;3) là tâm hình bình hành nên C(7;4) ;
. Vì I(3;3) là tâm hình bình hành nên C(7;4) ; ![]()
=> Đường thẳng ACcó pt là: x- 4y + 9= 0.
Do ![]() => Đường thẳng BC đi qua điểm C và có vtpt
=> Đường thẳng BC đi qua điểm C và có vtpt ![]() có pt là: 3x – y- 17= 0.
có pt là: 3x – y- 17= 0.
Khi đó :
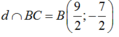
Ta có:
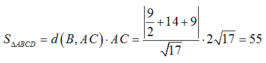

Câu 1: Chưa đủ dữ kiện để làm. Bạn xem lại đề.
Câu 2: Gọi tọa độ điểm H(a,b)
Ta có: \(\overrightarrow{AH}=(a-3; b-2); \overrightarrow{BC}=(1;8); \overrightarrow{BH}=(a-4; b+1); \overrightarrow{AC}=(2; 5)\)
Vì H là trực tâm tam giác ABC nên:
\(\left\{\begin{matrix} \overrightarrow{AH}.\overrightarrow{BC}=0\\ \overrightarrow{BH}.\overrightarrow{AC}=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a-3+8(b-2)=0\\ 2(a-4)+5(b+1)=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} a+8b=19\\ 2a+5b=3\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=\frac{-71}{11}\\ b=\frac{35}{11}\end{matrix}\right.\)

d/ Gọi P là trung điểm AB \(\Rightarrow P\left(3;\frac{1}{2}\right)\)
Trung trực của AB vuông góc AB nên nhận (2;1) là 1 vtpt
Phương trình trung trực AB:
\(2\left(x-3\right)+1\left(y-\frac{1}{2}\right)=0\Leftrightarrow4x+2y-13=0\)
Trung trực AC qua N và vuông góc AC nên nhận \(\left(1;-2\right)\) là 1 vtpt
Pt trung trực AC:
\(1\left(x-\frac{3}{2}\right)-2\left(y-1\right)=0\Leftrightarrow2x-4y+1=0\)
Tâm đường tròn ngoại tiếp là giao điểm 2 trung trực nên tọa độ là nghiệm:
\(\left\{{}\begin{matrix}4x+2y-13=0\\2x-4y+1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\frac{5}{2}\\y=\frac{3}{2}\end{matrix}\right.\)
e/ \(AB=\sqrt{5}\) ; \(AC=\sqrt{5}\) ; \(BC=\sqrt{10}\)
\(\Rightarrow AB^2+AC^2=BC^2\Rightarrow\Delta ABC\) vuông tại A
\(\Rightarrow cosB=\frac{AB}{BC}=\frac{\sqrt{5}}{\sqrt{10}}=\frac{1}{\sqrt{2}}\Rightarrow B=45^0\)
b/ Gọi M là trung điểm BC \(\Rightarrow M\left(\frac{5}{2};\frac{3}{2}\right)\Rightarrow\overrightarrow{AM}=\left(\frac{1}{2};\frac{3}{2}\right)=\frac{1}{2}\left(1;3\right)\)
\(\Rightarrow\) Đường thẳng AM nhận \(\left(3;-1\right)\) là 1 vtpt
Phương trình AM:
\(3\left(x-2\right)-1\left(y-0\right)=0\Leftrightarrow3x-y-6=0\)
c/N là trung điểm AC nên \(N\left(\frac{3}{2};1\right)\)
Đường thẳng MN song song BC nên nhận \(\left(1;3\right)\) là 1 vtpt
Phương trình MN:
\(1\left(x-\frac{3}{2}\right)+3\left(y-1\right)=0\Leftrightarrow x+3y-\frac{9}{2}=0\)

Gọi M là trung điểm BC . Ta có :
\(\left\{{}\begin{matrix}x_M=\frac{x_B+x_C}{2}=\frac{1+3}{2}=2\\y_M=\frac{y_B+y_C}{2}=\frac{2-4}{2}=-1\end{matrix}\right.\Rightarrow M\left(2;-1\right)\)
\(\overrightarrow{u_{AM}}=\left(2;-2\right)\Rightarrow\overrightarrow{n_{AM}}=\left(2;2\right)\)
PTTQ của AM : \(2\left(x-0\right)+2\left(y-1\right)=0\)
\(\Leftrightarrow x+y-1=0\)
Chọn A
A là giao điểm AB và AD nên tọa độ thỏa mãn: \(\left\{{}\begin{matrix}x-2y+3=0\\2x+y-4=0\end{matrix}\right.\) \(\Rightarrow A\left(1;2\right)\)
Đường thẳng AD nhận \(\left(2;1\right)\) là 1 vtpt
Do B thuộc AB nên tọa độ B có dạng \(B\left(2b-3;b\right)\) \(\Rightarrow\overrightarrow{CB}=\left(2b-7;b-1\right)\)
\(BC//AD\Leftrightarrow2\left(2b-7\right)+1\left(b-1\right)=0\Rightarrow b=3\)
\(\Rightarrow B\left(3;3\right)\) \(\Rightarrow\overrightarrow{BC}=\left(1;-2\right)\)
Mà \(\overrightarrow{BC}=\overrightarrow{AD}\Rightarrow D\left(2;0\right)\)