Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D M N Q P
Ta có: SAMP = \(\frac{1}{2}\)x AM x AP = \(\frac{1}{2}\)x (\(\frac{3}{4}\)x AB) x (\(\frac{1}{2}\) x AD) = (\(\frac{1}{2}\) x\(\frac{3}{4}\) x \(\frac{1}{2}\)) x AB x AD = \(\frac{3}{16}\)x SABCD = \(\frac{3}{16}\) x 192 = 36 cm2
SDPQ = \(\frac{1}{2}\) x PD x DQ = \(\frac{1}{2}\) x (\(\frac{1}{2}\)x AD) x (\(\frac{1}{2}\)x DC) = \(\frac{1}{8}\)x AD x DC = \(\frac{1}{8}\)x SABCD = \(\frac{1}{8}\)x 192 = 24 cm2
Tương tự, SNCQ = \(\frac{3}{20}\)x SABCD = 28,8 cm2 ; SBMN = \(\frac{1}{20}\)x SABCD = 9,6 cm2
=> SMNPQ = SABCD - ( SAMP + SDPQ + SNCQ + SBMN ) = 192 - (36 + 24 + 28,8 + 9,6) = 93,6 cm2
Vậy....

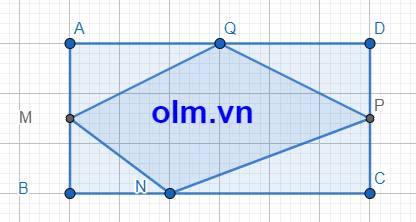
SAMQ = \(\dfrac{1}{2}\)AM\(\times\)AQ = \(\dfrac{1}{2}\times\) \(\dfrac{1}{2}\)AB\(\times\)\(\dfrac{1}{2}\)AD = \(\dfrac{1}{8}\)\(\times\)SABCD
SDPQ = \(\dfrac{1}{2}\)DQ\(\times\)DP = \(\dfrac{1}{2}\)\(\times\)\(\dfrac{1}{2}\) AD\(\times\)\(\dfrac{1}{2}\)DP = \(\dfrac{1}{8}\) \(\times\) SABCD
CN = CB - BN = CB - \(\dfrac{1}{3}\)CB = \(\dfrac{2}{3}\)CB
SCPN = \(\dfrac{1}{2}\)CP\(\times\)CN = \(\dfrac{1}{2}\)\(\times\)\(\dfrac{1}{2}\) CD\(\times\)\(\dfrac{2}{3}\)CB = \(\dfrac{1}{6}\)SABCD
SBNM = \(\dfrac{1}{2}\)BN\(\times\)BM = \(\dfrac{1}{2}\)\(\times\)\(\dfrac{1}{2}\)AB\(\times\)\(\dfrac{1}{3}\)BC = \(\dfrac{1}{12}\)SABCD
Diện tích tứ giác MNPQ bằng: (1 - \(\dfrac{1}{8}\) - \(\dfrac{1}{8}\) - \(\dfrac{1}{6}\) - \(\dfrac{1}{12}\) )SABCD = \(\dfrac{1}{2}\)SABCD
Diện tích của tứ giác MNPQ là: 240\(\times\)\(\dfrac{1}{2}\) = 120 (cm2)

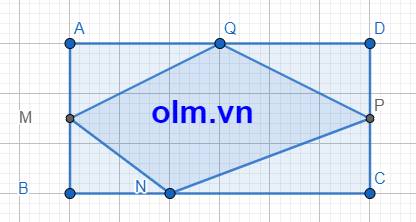
AM = BM = \(\dfrac{1}{2}\)AB; AQ = QD = \(\dfrac{1}{2}\) AD
SAMQ = \(\dfrac{1}{2}\)AM\(\times\)AQ =\(\dfrac{1}{2}\times\) \(\dfrac{1}{2}\)AB\(\times\)\(\dfrac{1}{2}\)AD = \(\dfrac{1}{8}\)SABCD = 240\(\times\)\(\dfrac{1}{8}\)=30(cm2)
DQ = QA = \(\dfrac{1}{2}\)AD; DP = PC = \(\dfrac{1}{2}\) DC
SDPQ =\(\dfrac{1}{2}\times\)DP\(\times\) DQ =\(\dfrac{1}{2}\) \(\times\)\(\dfrac{1}{2}\)AD\(\times\)\(\dfrac{1}{2}\)DC =\(\dfrac{1}{8}\)SABCD = 240\(\times\)\(\dfrac{1}{8}\)=30(cm2)
CN = BC - BN = BC - \(\dfrac{1}{3}\)BC = \(\dfrac{2}{3}\)BC
SCPN = \(\dfrac{1}{2}\)CP\(\times\)CN= \(\dfrac{1}{2}\)\(\times\) \(\dfrac{1}{2}\)CD \(\times\) \(\dfrac{2}{3}\) BC = \(\dfrac{1}{6}\)SABCD=240\(\times\dfrac{1}{6}\)=40 (cm2)
SBMN=\(\dfrac{1}{2}\) BM\(\times\)BN =\(\dfrac{1}{2}\times\dfrac{1}{2}\)AB\(\times\)\(\dfrac{1}{3}\)BC=\(\dfrac{1}{12}\)SABCD=240\(\times\)\(\dfrac{1}{12}\)=20(cm2)
Diện tích tứ giác MNPQ là:
240 - (30 + 30 + 40 + 20) = 120(cm2)
Đáp số: 120 cm2

A B C D M N P Q
Hình tớ vẽ hơi xấu, bạn thông cảm nhé.
Ta có \(S\Delta AMQ=\dfrac{1}{2}.AM.AQ=\dfrac{1}{2}.\dfrac{1}{2}AB.\dfrac{1}{3}AD\)
\(=\dfrac{1}{12}.288=24\left(cm^2\right)\)
\(S\Delta MBN=\dfrac{1}{2}MB.BN=\dfrac{1}{2}.\dfrac{1}{2}AB.\dfrac{1}{4}BC\)
\(=\dfrac{1}{16}.288=18\left(cm^2\right)\)
\(S\Delta QDP=\dfrac{1}{2}QD.DP=\dfrac{1}{2}.\dfrac{2}{3}AD.\dfrac{2}{3}DC\)
\(=\dfrac{2}{9}.288=64\left(cm^2\right)\)
\(S\Delta NPC=\dfrac{1}{2}.NC.CP=\dfrac{1}{2}.\dfrac{3}{4}BC.\dfrac{1}{3}.DC\)
\(=\dfrac{1}{8}.288=36\left(cm^2\right)\)
\(S_{MNPQ}=288-36-64-18-24=146\left(cm^2\right)\)
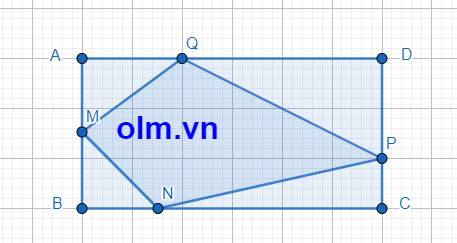
DQ + QA = DA ⇒ QA = DA - DQ = DA - \(\dfrac{2}{3}\)DA = \(\dfrac{1}{3}\)DA
SAMQ = \(\dfrac{1}{3}\)SADM( Vì hai tam giác có chung chiều cao hạ từ đỉnh M xuống đáy AD và AQ = \(\dfrac{1}{3}\)AD)
SADM = \(\dfrac{1}{2}\)SABD(vì hai tam giác có chung chiều cao hạ từ đỉnh D xuống đáy AB và AM = \(\dfrac{1}{2}\)AB)
SABD = \(\dfrac{1}{2}\)SABCD(vì ABCD là hình chữ nhật)
⇒SAMQ = \(\dfrac{1}{3}\times\dfrac{1}{2}\times\dfrac{1}{2}\)\(\times\)SABCD = 288 \(\times\) \(\dfrac{1}{12}\)= 24 (cm2)
SDPQ = \(\dfrac{2}{3}\)SADP(vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy AD và DQ = \(\dfrac{2}{3}\)DA)
DP = DC - CP = DC - \(\dfrac{1}{3}\)DC = \(\dfrac{2}{3}\)DC
SADP = \(\dfrac{2}{3}\)SACD(Vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy DC và DP = \(\dfrac{2}{3}\) DC)
SACD = \(\dfrac{1}{2}\)SABCD
⇒SDPQ = \(\dfrac{2}{3}\times\dfrac{2}{3}\times\)\(\dfrac{1}{2}\)\(\times\)SABCD = 288 \(\times\) \(\dfrac{2}{9}\)= 64 (cm2)
CN = BC - BN = BC - \(\dfrac{1}{4}\)BC = \(\dfrac{3}{4}\)BC
SCNP = \(\dfrac{3}{4}\)SCBP(vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy BC và CN = \(\dfrac{3}{4}\)BC)
SCBP = \(\dfrac{1}{3}\)SBCD(vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đấy CD và CP = \(\dfrac{1}{3}\) CD)
SBCD = \(\dfrac{1}{2}\)SABCD (vì ABCD là hình chữ nhật)
⇒SCNP = \(\dfrac{3}{4}\times\dfrac{1}{3}\times\dfrac{1}{2}\) SABCD = 288 \(\times\) \(\dfrac{1}{8}\) = 36 (cm2)
SBMN = \(\dfrac{1}{4}\)SBCM (Vì hai tam giác có chung đường cao hạ từ đỉnh M xuống đáy BC và BN = \(\dfrac{1}{4}\)BC)
SBCM = \(\dfrac{1}{2}\)SABC(Vì hai tam giác có chung chiều cao hạ từ đỉnh C xuống đáy AB và BM =\(\dfrac{1}{2}\)AB)
SABC = \(\dfrac{1}{2}\)SABCD(vì ABCD là hình chữ nhật)
⇒ SBMN = \(\dfrac{1}{4}\times\dfrac{1}{2}\times\dfrac{1}{2}\)\(\times\)SABCD = 288 \(\times\)\(\dfrac{1}{16}\) = 18 (cm2)
SMNPQ = SABCD - (SAMQ +SDPQ+SCNP+SBMN)
Diện tích của MNPQ là:
288 - (64 + 24 + 36 + 18) = 146 (cm2)
Đáp số: 146 cm2