Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

V, h nó mới được như cũ, để t vt lại cho dễ nhìn
gọi a,b là 2 độ dài của hình chữ nhật
ta có BĐT cần chứng minh
<=>\(2\left(a+b\right)\ge\frac{32ab}{2ab+2\left(a+b\right)+2}\Leftrightarrow a+b\ge\frac{8ab}{ab+\left(a+b\right)+1}\)
<=>\(ab\left(a+b\right)+\left(a+b\right)^2+a+b\ge8ab\)
<=>\(\left(ab+1\right)\left(a+b\right)+\left(a+b\right)^2\ge8ab\)
ta luôn có \(\left(a+b\right)^2\ge4ab\)
mà \(a+b\ge2\sqrt{ab};ab+1\ge2\sqrt{ab}\) =>\(\left(a+b\right)\left(ab+1\right)\ge4ab\)
+ vào thì ta sẽ ra đpcm
^_^
:V, OLM bị lỗi, t vt như vầy cố dịch nhé !
Ta có BĐT <=>2(a+b)>=32ab/[2ab+2(a+b)+2]
<=>a+b>=8ab/ab+a+b+1
quy đồng, rồi, ta có
(a+b)^2+(ab+1)(a+b)>=8ab
Áp dụng bđt cô-si, ta chứng minh được (a+b)^2 >=4ab
mà (ab+1)>=2.căn(ab); a+b>=2.căn(ab)
nhân vào, ta có (ab+1)(a+b)>=4ab
+ thêm cái kia, ta có BĐT cần phải chứng minh (ĐPCM)
^_^

Sau khi tăng kích thước của mỗi chiều, ta được hình chữ nhật A’B’C’D’ có chiều dài A’B’ = (40 + x) cm, chiều rộng B’C’ = (25 + x) cm.
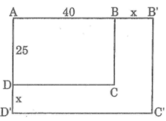
Diện tích hình chữ nhật mới:
S = (40 + x)(25 + x) = 1000 + 65x + x 2
S không phải là hàm số bậc nhất đối với x vì có bậc của biến số x là bậc hai.
Chu vi hình chữ nhật mới:
P = 2.[(40 + x) + (25 + x)] = 4x + 130
P là hàm số bậc nhất đối với x có hệ số a = 4, hệ số b = 130.

a: \(S=\left(30-x\right)\left(40-x\right)\)
\(=\left(x-30\right)\left(x-40\right)=x^2-70x+1200\)
=>S không là hàm số bậc nhất đối với x
\(P=2\left[30-x+40-x\right]=2\left(70-2x\right)=-4x+140\)
=>P là hàm số bậc nhất đối với x
b: Khi x=0 thì \(P=-4\cdot0+140=140\)
Khi x=1 thì \(P=140-4=136\)
Khi x=2 thì \(P=140-8=132\)
Khi x=3 thì \(P=140-12=128\)
Khi x=4 thì P=140-4*4=124

Sau khi tăng kích thước của mỗi chiều, ta được hình chữ nhật A’B’C’D’ có chiều dài A’B’ = (40 + x) cm, chiều rộng B’C’ = (25 + x) cm.
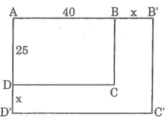
Các giá trị tương ứng của P:
| x | 0 | 1 | 1,5 | 2,5 | 3,5 |
| P = 4x + 130 | 130 | 134 | 136 | 140 | 144 |

Gọi chiều dài và chiều rộng của thửa ruộng lần lượt là a(m) và b(m)(Điều kiện: a>0; b>0; \(a\ge b\))
Vì chu vi của thửa ruộng là 120m nên ta có:
2(a+b)=120
hay a+b=60(1)
Diện tích ban đầu là:
\(ab\left(m^2\right)\)
Vì khi giảm chiều dài đi 10m và tăng chiều rộng 10m thì diện tích không thay đổi nên ta có phương trình:
\(\left(a-10\right)\left(b+10\right)=ab\)
\(\Leftrightarrow ab+10a-10b-100=ab\)
\(\Leftrightarrow10a-10b=100\)
hay a-b=10(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}a+b=60\\a-b=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a=70\\a-b=10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=35\\35-b=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=35\\b=25\end{matrix}\right.\)(thỏa ĐK)
Diện tích hình chữ nhật là:
\(S=ab=35\cdot25=875\left(m^2\right)\)
Gọi chiều dài của thửa ruộng là x (10<x<200) \(\Rightarrow\) chiều rộng là \(200-x\) (m)
Diện tích thửa ruộng ban đầu: \(x\left(200-x\right)\)
Diện tích thửa ruộng lúc sau: \(\left(x-10\right)\left(210-x\right)\)
Theo bài ra ta có pt:
\(x\left(200-x\right)=\left(x-10\right)\left(210-x\right)\)
\(\Leftrightarrow20x=2100\)
\(\Rightarrow x=105\)
Diện tích thửa ruộng: \(105\left(200-105\right)=...\)

Gọi a,b là chiều dài và chiều rông
Ta có: \(\hept{\begin{cases}a+b=\frac{80}{2}=40\\3b+5=2a\end{cases}}\)
Từ đây: a=40-b
Thế vô:
\(120-3a+5=2a\)
Suy ra: a=25
Suy ra: b=15
Vậy S=375 m2