Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác ABC có:
MA=MB ( gt)
NC=NB(gt)
=> MN là đường trung bình của tam giác ABC
Nên MN = AC:2 và MN // AC (1)
Xét tam giác ACD có QA=QD(gt)
ID=IC(gt)
=> QI là đường trung bình của tam giác ACD
nên IQ= AC:2 và IQ // AC (2)
từ 1 và 2 => QI=MN
QI // MN
=> tứ giác MN là hình bình hành ( 2 cạnh đối // và = nhau)
mà AC vuông góc với BD tại O
=> MN vuông góc với QM hay góc QMN= 90 độ
từ 3 và 4 => MNIQ là hình chữ nhật ( hình bình hành có1 góc vuông )

Tứ giác có thể là hình vuông, chữ nhật phải không bạn?
P/s: Hỏi thôi chớ không trả lời đâu :D

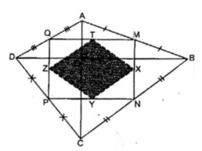
Trong △ ABD ta có:
M là trung điểm của AB
Q là trung điểm của AD nên MQ là đường trung bình của △ ABD.
⇒ MQ // BD và MQ = 1/2 BD (tính chất đường trung bình của tam giác) (1)
Trong △ CBD ta có:
N là trung điểm của BC
P là trung điểm của CD
nên NP là đường trung bình của △ CBD
⇒ NP // BD và NP = 1/2 BD (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: MQ // NP và MQ = NP nên tứ giác MNPQ là hình bình hành
AC ⊥ BD (gt)
MQ // BD
Suy ra: AC ⊥ MQ
Trong △ ABC có MN là đường trung bình ⇒ MN // AC
Suy ra: MN ⊥ MQ hay (NMQ) = 90 0
Vậy tứ giác MNPQ là hình chữ nhật.

Bài 3:
a: Ta có: \(\widehat{OAB}=\widehat{ODC}\)
\(\widehat{OBA}=\widehat{OCD}\)
mà \(\widehat{ODC}=\widehat{OCD}\)
nên \(\widehat{OAB}=\widehat{OBA}\)
Xét ΔOAB có \(\widehat{OAB}=\widehat{OBA}\)
nên ΔOAB cân tại O
A B C D O
Ta có: ABCD là hình chữ nhật mà AC \(\perp\) BD
=> ABCD là hình vuông (hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông)
=> AB = BC = CD = DA (tính chất hình vuông)
Vậy AB = BC = CD = DA (đpcm)