Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Delta ABD\)vuông tại A \(\Rightarrow\)Theo định lý Pytago ta có: \(AB^2+AD^2=BD^2\)(1)
mà \(AD=\frac{3}{4}AB\), \(BD=10cm\)
Từ (1) \(\Rightarrow AB^2+\left(\frac{3}{4}AB\right)^2=10^2\)\(\Leftrightarrow AB^2+\frac{9}{16}AB^2=100\)
\(\Leftrightarrow AB^2\left(1+\frac{9}{16}\right)=100\)\(\Leftrightarrow AB^2.\frac{25}{16}=100\)\(\Leftrightarrow AB^2=64\)
\(\Rightarrow AB=8cm\)\(\Rightarrow AD=6cm\)
\(\Rightarrow S_{ABCD}=AB.AD=8.6=48\left(cm^2\right)\)

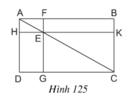
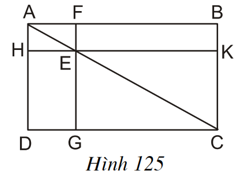
Ta có: SEHDG = SADC – SAHE – SEGC.
SEFBK = SABC – SAFE – SEKC.
Để chứng minh SEHDG = SEFBK,
ta đi chứng minh SADC = SABC; SAHE = SAFE ; SEGC = SEKC.
+ Chứng minh SADC = SABC.
SADC = AD.DC/2;
SABC = AB.BC/2.
ABCD là hình chữ nhật ⇒ AB = CD, AD = BC
⇒ SADC = SABC.
+ Chứng minh SAHE = SAFE (1)
Ta có: EH // AF và EF // AH
⇒ AHEF là hình bình hành
Mà Â = 90º
⇒ AHEF là hình chữ nhật
⇒ SAHE = SAFE (2)
+ Chứng minh SEGC = SEKC
EK // GC, EG // KC
⇒ EGCK là hình bình hành
Mà D̂ = 90º
⇒ EGCK là hình chữ nhật
⇒ SEGC = SEKC (3).
Từ (1); (2); (3) suy ra đpcm.

1. Áp dụng định lý Pi-ta-go ta có:
\(AB^2+BC^2=AC^2\Rightarrow BC=\sqrt{10^2-8^2}=6cm\)
Diện tích hình chữ nhật là:\(AB.BC=8.6=48cm^2\)
2.B

BH=căn 10^2-6^2=8cm
=>BD=10^2/8=12,5cm
=>AD=7,5cm
S ABCD=7,5*10=75cm2

Tương tự bài 2A ta có S M B C D N = S A B C D − S A M N = 60 − 1 2 ( 10 − x ) . ( 6 − x )

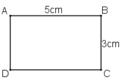
a) Hình chữ nhật ABCD đã cho có diện tích là SACBD = 3.5 = 15 (cm2)
Hình chữ nhật có kích thước là 1cm x 12cm có diện tích là 12cm2 và chu vi là (1 + 12).2 = 26 (cm) (có 26 > 15)
Hình chữ nhật kích thước 2cm x 7cm có diện tích là 14cm2 và chu vi là (2 + 7).2 = 18 (cm)
(có 18 > 15).
Như vậy, vẽ được nhiều hình chữ nhật có diện tích bé hơn nhưng có chu vi lớn hơn hình chữ nhật ABCD cho trước.
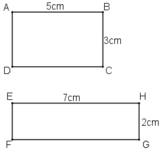
b) + Chu vi hình chữ nhật ABCD đã cho là (5 + 3).2 = 16 cm
Cạnh hình vuông có chu vi bằng chu vi hình chữ nhật ABCD là: 16 : 4 = 4 cm
Diện tích hình vuông này là 4.4 = 16 cm2
(Ở trên hình là ví dụ hình vuông MNPQ có cạnh là 4cm)
Vậy SHCN < SHV
+ Trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.
Gọi cạnh của hình chữ nhật có độ dài lần lượt là a, b.
Hình vuông có cùng chu vi với hình chữ nhật nên cạnh hình vuông là 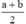
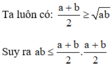
⇒ Hình vuông có diện tích lớn nhất.

a) Diện tích đáy hình hộp chữ nhật:
AB.AC=10.20=200(cm2)AB.AC=10.20=200(cm2)
Thể tích hình hộp chữ nhật:
V=S.h=200.15=3000(cm3)V=S.h=200.15=3000(cm3)
b) tam giác A'B'C' vuông tại B. Áp dụng định lý PITAGO ta có:
A′C′=√A′B′2+B′C′2=√102+202=10√5(cm)A′C′=A′B′2+B′C′2=102+202=105(cm)
⇒AC′=√AA′+A′C′2=√152+102.5=5√29(cm)

a) Diện tích hình chữ nhật ABCD là:
SABCD = 12.16= 192 ( cm2)
b) Áp dụng định lý Py-ta-go trong tam giác ADC vuông tại A :
AD2 + DC2 = AC2
122 + 162 = AC2
400 = AC2
=> AC = 20 (cm)
HCN ABCD có O là giao điểm hai đường chéo AC và BD nên O là trung điểm của AC và BD.
Xét tam giác ADC vuông tại D có O là trung điểm AC
=> DO = 1/2 AC = 1/2 . 20 = 10 ( cm )
Tam giác ADC vuông tại D có O là trung điểm AC
M là trung điểm AD
=> MO là đường trung bình của tam giác ADC
=> MO = 1/2 DC
=> MO = 1/2 . 16 = 8 ( cm)

Áp dụng định lý Pi-ta-go vào tam giác ADC vuông tại D
DC =\(\sqrt{AC^2-AD^2}\)=\(\sqrt{10^2-6^2}\)=8 cm
diện tích hcn là :AD.DC=6.8=48 cm2