Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Vì ABCD là hình chữ nhật nên AB// DC => góc ABD = BDC ( hai góc đối đỉnh)
Xét tam giác AHB và tam giác BCD có
góc AHB = góc BCD =90 ĐỘ
góc ABD = BDC ( cmtrên)
Suy ra .............( g.g)
Vì ABCD là hcn nên AB =DC =20
BC=AD=15
Theo định lí Pitago trong tam giác BCD
\(BD^2=BC^2+DC^2\)
\(BD^2=20^2+15^2\)
\(BD^2=625\)
BD = 25
Theo a ta có \(\frac{AH}{AB}=\frac{BC}{BD}\)
NÊN \(AH=\frac{AB\cdot BC}{BD}\)
\(AH=\frac{20\cdot15}{25}\)
AH=12
c, d tự trả lời
e hình như dựa một chút vào tình chất đường phân giác trong tam giác

a)
vì ABCD hình chữ nhật nên ta có AB//CD
=> góc ABH= góc BDC ( so le trong, AB//CD)
xét tam giác AHB,BCD có
góc A= góc C =90
góc ABH=BDC(cmt)
=> tam giác AHB đồng dạng với tam giác CDB (gg)
b)
vì ABCD hcn nên
AB=CD=12
BC=AD=9
AD Đlí pytado cho tam giác vuông CDB có
BD2=BC2+DC2
BD2=81+144
BD=15cm
theo câu a) ta có
AH/AB=BC/BD
=> AH= AB.BC chia BD
AH= 12.9 chia 15
AH= 7.2CM
C)
BD
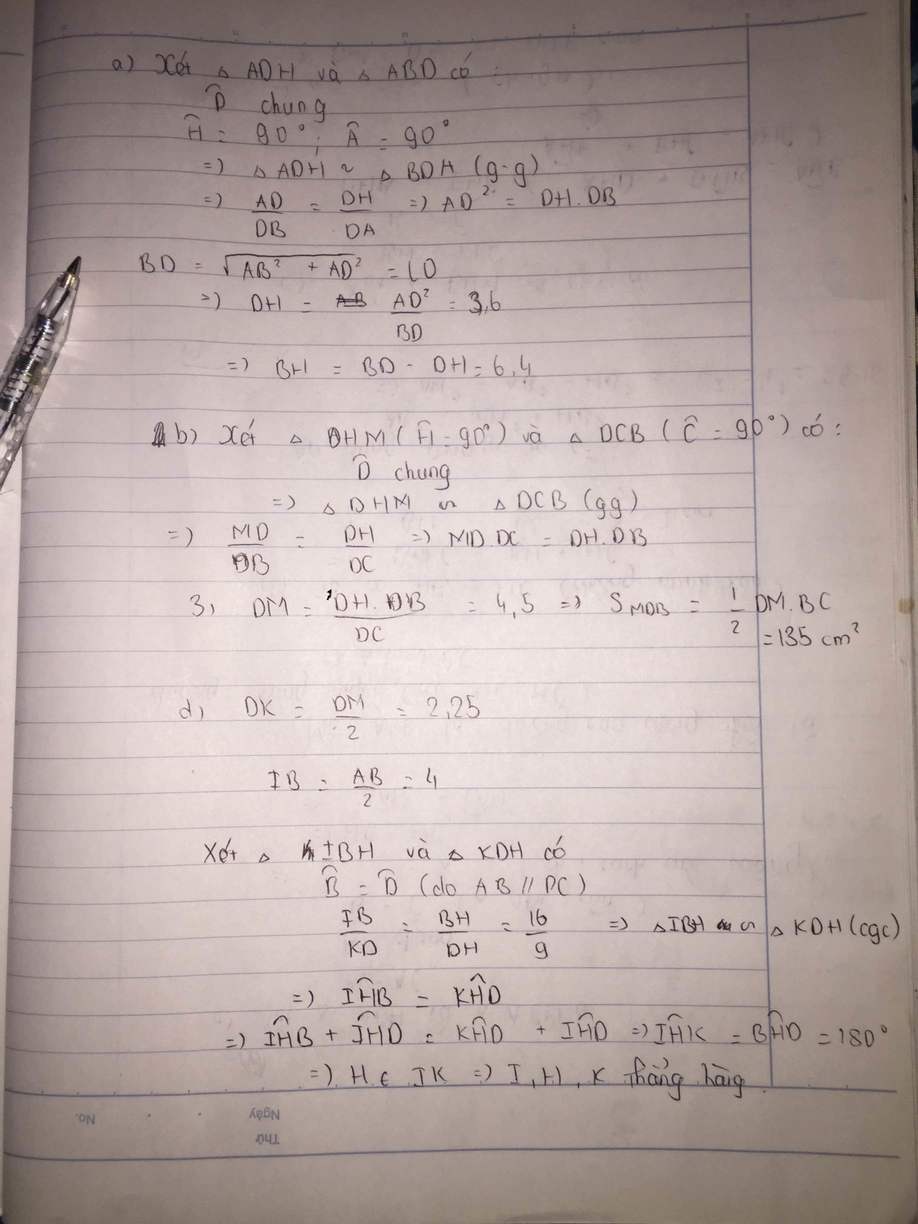
A B C D H M 8 6
a. Tam giác ABD vuông tại A
⇒BD2 = AD2 + AB2
⇒BD2 = 62 + 82
⇒BD = 10 (cm)
b. Xét ΔAHB và ΔMHD có:
Góc AHB = MHD = 90o
Góc ABH = BDH ( so le trong)
Do đó: ΔAHB ~ ΔMHD (g.g)
c. Xét ΔMHD và ΔBCD có:
Góc MHD = BCD = 90o
Góc D chung
Do đó: ΔMHD ~ ΔBCD (g.g)
\(\Rightarrow\dfrac{MD}{BD}=\dfrac{HD}{CD}\Rightarrow MD.CD=HD.BD\)
d. Ta có: ΔAHB ~ ΔDAB
\(\Rightarrow\dfrac{AH}{DA}=\dfrac{AB}{BD}\Rightarrow AH=\dfrac{DA.AB}{BD}=\dfrac{6.8}{10}=4,8\)
Ta có: ΔABH vuông tại H
⇒AB2 = AH2 + BH2
⇒BH2 = AB2 - AH2
⇒BH2 = 82 - 4,82
⇒BH = 6,4 (cm)
Ta có: HD = BD - BH = 10 - 6,4 = 3,6 (cm)
Ta có: ΔMHD ~ ΔBCD
⇒ \(\dfrac{MH}{BC}=\dfrac{HD}{CD}\Rightarrow MH=\dfrac{BC.HD}{CD}=\dfrac{6.3,6}{8}=2,7\left(cm\right)\)
\(S_{\Delta MDB}=\dfrac{MH.DB}{2}=\dfrac{2,7.10}{2}=13,5\left(cm^2\right)\)
Cảm ơn bạn na