Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.Diện tích tam giác ABD = 1/2 diện tích tam giác DBC vì đáy AB = 1/2 đáy CD và 2 chiều cao cùng là chiều cao của hình thang.
=> Diện tích tam giác ABD = 1 phần và diện tích tam giác DBC = 2 phần. ( Tự vẽ hình theo lời giải này ).
Diện tích tam giác ABD là : 105 : (1 + 2) . 1 = 35 (cm2)
b.Diện tích tam giác ABD = diện tích tam giác ABC vì chung đáy AB và 2 chiều cao cùng là chiều cao của hình thang.
Ta có: Diện tích ABD - diện tích ABO = Diện tích ABC - diện tích ABO.
<=> Diện tích AOD = Diện tích BOC.
Diện tích tam giác BDC là : 105 - 35 = 70 (cm2)
Vì diện tích tam giác DBC gấp 2 lần diện tích tam giác ABD mà chung đáy DB nên => chiều cao hạ từ C xuống đáy DB gấp 2 lần chiều cao hạ từ A xuống đáy DB. ( Tự vẽ hình theo lời giải ).
Mà diện tích tam giác AOD = diện tích tam giác BOC , chiều cao hạ từ C xuống đáy DB gấp 2 lần chiều cao hạ từ A xuống đáy DB nên đáy DO phải gấp 2 lần đáy OB để diện tích hai hình bằng nhau.
Vì đáy DO gấp 2 lần đáy OB mà chung chiều cao hạ từ A nên diện tích tam giác ADO gấp 2 lần diện tích tam giác AOB.
Vì diện tích tam giác AOD = diện tích tam giác BOC nên diện tích tam giác BOC cũng bằng 2 lần diện tích tam giác AOB.
Vì chung chiều cao hạ từ B mà diện tích tam giác BOC gấp 2 lần diện tích tam giác AOB nên đáy OA = 1/2 đáy OC.
Đáp số : a.35 cm2.
b.OA = 1/2 OC.

A B C D O (hình minh hoạ)
a)
Theo đề ra: \(AB=\dfrac{1}{2}CD\)
Đường cao kẻ từ D đến AB bằng đường cao kẻ từ B dến CD vì đều là đường cao của hình thang ABCD
\(\Rightarrow S_{ABC}=\dfrac{1}{2}SBCD\)
mà hai hình tam giác này có chung đáy BD
\(\Rightarrow\) Đường cao kẻ từ A đến \(BD=\dfrac{1}{2}\) đường cao kẻ từ C đến BD, hay đường cao kẻ từ A đến \(BO=\dfrac{1}{2}\) đường cao kẻ từ C đến BO
Vì chung đáy BO, đường cao kẻ từ A đến \(BO=\dfrac{1}{2}\) đường cao kẻ từ C đến BO
\(\Rightarrow S_{ABO}=\dfrac{1}{2}S_{BOC}\)
mà hai hình tam giác này có chung đường cao kẻ từ B đến AC
\(\Rightarrow AO=\dfrac{1}{2}CO\)
b)
Theo phần a), \(S_{ABO}=\dfrac{1}{2}S_{BOC}\)
\(S_{BOC}=1\times2=2cm^2\)
\(S_{ABC}=1+2=3cm^2\)
Mà \(AB=\dfrac{1}{2}CD\), đường cao kẻ từ C đến AB bằng đường cao kẻ từ A đến CD đều là đường cao của hình thang ABCD
\(\Rightarrow S_{ABC}=\dfrac{1}{2}S_{ACD}\)
\(S_{ACD}=3\times2=6cm^2\)
\(S_{ABCD}==6+3=9cm^2\).

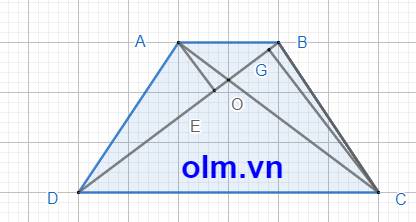
a, Dựng chiều cao CG của \(\Delta\)BCD và chiều cao AE của \(\Delta\) ABD
\(\dfrac{S_{ABD}}{S_{BCD}}\) = \(\dfrac{AE}{CG}\) (vì hai tam giác có chung cạnh đáy BD nên tỉ số diện tích là tỉ số hai chiều cao tương ứng)
\(\dfrac{S_{ABD}}{S_{BCD}}\) = \(\dfrac{AB}{CD}\) (vì hai tam giác có chiều cao bằng nhau nên tỉ số diện tích hai tam giác là tỉ số hai cạnh đáy)
⇒ \(\dfrac{AE}{CG}\) = \(\dfrac{AB}{CD}\) = \(\dfrac{1}{3}\)
\(\dfrac{S_{AOB}}{S_{BOC}}\) = \(\dfrac{AE}{CG}\) ( hai tam giác có chung cạnh đáy OB nên tỉ số diện tích là tỉ số hai chiều cao tương ứng)
\(\dfrac{S_{AOB}}{S_{BOC}}\) = \(\dfrac{AO}{OC}\) ( vì hai tam giác có chiều cao bằng nhau nên tỉ số diện tích là tỉ số hai cạnh đáy)
⇒ \(\dfrac{AE}{CG}\) = \(\dfrac{AO}{OC}\) = \(\dfrac{1}{3}\)
Chứng minh tương tự ta có: \(\dfrac{BO}{OD}\) = \(\dfrac{1}{3}\)
b, SABD = SABC ( vì hai tam giác có chung cạnh đáy AB và hai chiều cao bằng nhau)
SABD = SABO + SAOD = SAOB + SBOC = SABC
SAOD \(\times\) 1 = SBOC
SAOD \(\times\) 1 = SAOD
SAOD \(\times\) \(\dfrac{1}{3}\) = SAOB (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BD và \(\dfrac{OB}{OD}\) = \(\dfrac{1}{3}\))
SAOD \(\times\) 3 = SDOC ( vì hai tam giác có chung chiều cao hạ từ đỉnh D xuống đáy AC và \(\dfrac{AO}{OC}\) =\(\dfrac{1}{3}\))
Cộng các vế trên ta với nhau ta có diện tích hình thang ABCD bằng:
1 + 1 + \(\dfrac{1}{3}\) + 3 = \(\dfrac{16}{3}\) ( diện tích hình tam giác AOD)
Diện tích tam giác AOD là: 32 : \(\dfrac{16}{3}\) = 6 (m2)
ĐS...
Mọi ng giải nhanh giúp mình nhé, mình đag cần gấp lắm, mai đi học r, cảm ơn mng nh🥹
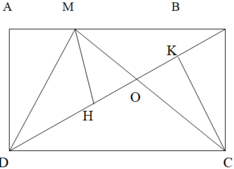

do 2 đường chéo hình chữ nhật cắt nhau tại trung điểm mỗi đường
nên OA=OB=OC=OD
**** cho mk nha