Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) () // (ABCD) =>
// AB =>
là trung điểm của SB. Chứng minh tương tự với các điểm còn lại
b) Áp dụng định lí Ta-lét trong không gian:
\(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}\).
Do \(A_1A_2=A_2A\) nên : \(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}=1\).
Nên \(B_1B_2=B_2B;C_1C_2=CC_2=D_1D_2=D_2D\).
c) Có hai hình chóp cụt:

Xét ΔSAB có \(\dfrac{SM}{SA}=\dfrac{SN}{SB}=\dfrac{1}{2}\)
nên MN//AB
Xét ΔSBC có \(\dfrac{SN}{SB}=\dfrac{SP}{SC}=\dfrac{1}{2}\)
nên NP//CD
Xét ΔSDC có \(\dfrac{SP}{SC}=\dfrac{SQ}{SD}=\dfrac{1}{2}\)
nên PQ//CD
MN//AB
AB\(\subset\left(ABCD\right)\)
MN không nằm trong mp(ABCD)
Do đó: MN//(ABCD)
NP//BC
BC\(\subset\)(ABCD)
NP không nằm trong mp(ABCD)
Do đó: NP//(ABCD)
PQ//CD
CD\(\subset\)(ABCD)
PQ không nằm trong mp(ABCD)
Do đó: PQ//(ABCD)
MN//(ABCD)
NP//(ABCD)
MN,NP cùng nằm trong mp(MNP)
Do đó: (MNP)//(ABCD)
NP//(ABCD)
PQ//(ABCD)
NP,PQ cùng nằm trong mp(NPQ)
Do đó: (NPQ)//(ABCD)
(MNP)//(ABCD)
(NPQ)//(ABCD)
Do đó: M,N,P,Q đồng phẳng

Em kiểm tra lại đề, \(\left(\alpha\right)\) đi qua AI nên nó không thể cắt SA tại M được nữa (vì nó đi qua A nên đã cắt SA tại A rồi)
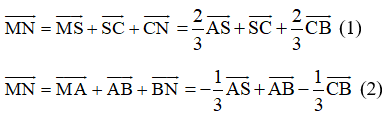
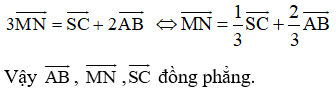


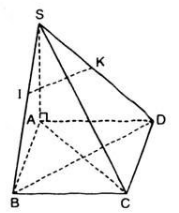
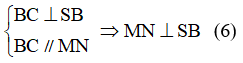
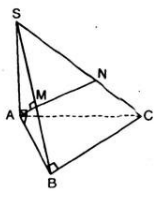



Xét tam giác SAD có: \(\dfrac{MA}{MS}=\dfrac{QD}{QS}\) suy ra MQ // AD do đó MQ // (ABCD)
Tương tự ta có: QP // (ABCD)
Vậy mp(MPQ) // mp(ABCD).
Lập luận tương tự, ta có mp(NPQ) // (ABCD).
Hai mặt phẳng (MPQ) và (NPQ) cùng đi qua điểm P và cùng song song với mặt phẳng (ABCD) nên hai mặt phẳng đó trùng nhau, tức bốn điểm M, N, P, Q đồng phẳng.