Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
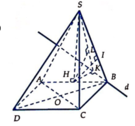
Vẽ đường thẳng d qua B và song song với AC.
Gọi K, I lần lượt là hình chiếu của H trên d và SB, L là hình chiếu của H trên SK.
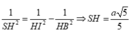
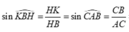
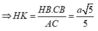
![]()
![]()
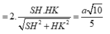

Kẻ \(SH\perp AB\Rightarrow SH\perp\left(ABCD\right)\)
Trong mp (ABCD), qua H kẻ đường thẳng song song AD cắt CD tại K
\(\Rightarrow\left\{{}\begin{matrix}AB\perp\left(SHK\right)\\CD\perp\left(SHK\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left(SHK\right)\perp\left(SAB\right)\\\left(SHK\right)\perp\left(SCD\right)\end{matrix}\right.\)
\(\Rightarrow\widehat{HSK}\) là góc giữa (SAB) và (SCD)
Ta có:
\(SB=\sqrt{AB^2-SA^2}=a\sqrt{3}\Rightarrow SH=\dfrac{SA.SB}{AB}=\dfrac{a\sqrt{3}}{2}\); \(HK=AD=2a\)
\(tan\widehat{HSK}=\dfrac{HK}{SH}=\dfrac{4\sqrt{3}}{3}\Rightarrow\widehat{HSK}\approx66^035'\)

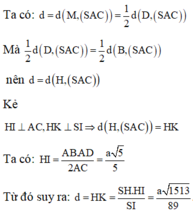

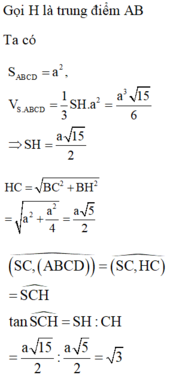
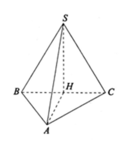


SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy. Góc giữa SD và đáy bằng bao nhiêu?
Trả lời:
Đề bài chưa đủ dữ kiện để xác định chính xác góc này (cần biết vị trí S so với đáy).
Nếu bạn bổ sung thêm thông tin về vị trí điểm S (ví dụ S nằm trên đường vuông góc qua A hoặc B của đáy), mình sẽ giải chi tiết cho bạn!