Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

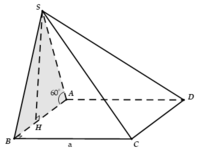
Gọi H là điểm gia của AC và MD.
Ta có : (SAC) giao (SMD) = SH, cùng vuông góc vuối (ABCD)
=> SH là đường cao.
Kẻ HK vuông góc với AB, có AB vuông góc với (SKH) => góc tạo bởi (ABCD) và (SAB)
=> SKH = 600
Có tam giác ABD đều tại A => AO = \(\frac{a\sqrt{3}}{8}\)
=> tan (SKH) = SH/SK => SH = \(\frac{3a}{8}\Rightarrow V=\frac{\sqrt{3}a^3}{16}\)
=> cos OM và OA là \(\frac{a\sqrt{13}}{4}\)

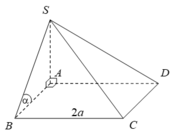
Ta có: SA ⊥ (ABCD) SA ⊥ AB
Mặt phẳng (SAB) tạo với đáy một góc 60° nên
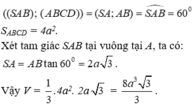

Lời giải:
Vì $(SAB), (SAD)$ cùng vuông góc với $(ABCD)$ mà $(SAB)\cap (SAD)\equiv SA$ nên $SA\perp (ABCD)$
Vì $SA\perp (ABCD)$ nên $SA\perp CB$
Mà: $AB\perp CB$
$\Rightarrow CB\perp (SAB)$
$\Rightarrow \angle (SC,(ABCD))=\angle (SC, SB)=\angle CSB=45^0$
$\Rightarrow SB=CB=a$
$SA=\sqrt{SB^2-AB^2}=\sqrt{a^2-a^2}=0$ (vô lý)

Dễ dàng chứng minh \(BC\perp BD\) (Pitago đảo) \(\Rightarrow BC\perp\left(SBD\right)\)
Đồng thời dễ dàng chứng minh \(AB\perp\left(SAD\right)\)
Từ D kẻ \(DH\perp SA\Rightarrow DH\perp\left(SAB\right)\)
Từ D kẻ \(DK\perp SB\Rightarrow DK\perp\left(SBC\right)\)
\(\Rightarrow\widehat{HDK}\) là góc giữa (SAB) và (SBC)
\(\Rightarrow\widehat{HDK}=30^0\Rightarrow DH=DK.cos30^0=\dfrac{DK\sqrt{3}}{2}\Rightarrow DH^2=\dfrac{3DK^2}{4}\)
Hệ thức lượng: \(\dfrac{1}{DH^2}=\dfrac{1}{SD^2}+\dfrac{1}{AD^2}\Leftrightarrow\dfrac{4}{3DK^2}=\dfrac{1}{SD^2}+\dfrac{1}{a^2}\Rightarrow\dfrac{1}{DK^2}=\dfrac{3}{4SD^2}+\dfrac{3}{4a^2}\) (1)
\(\dfrac{1}{DK^2}=\dfrac{1}{SD^2}+\dfrac{1}{BD^2}=\dfrac{1}{SD^2}+\dfrac{1}{2a^2}\) (2)
(1);(2) \(\Rightarrow\dfrac{3}{4SD^2}+\dfrac{3}{4a^2}=\dfrac{1}{SD^2}+\dfrac{1}{2a^2}\Rightarrow SD=a\)
\(V=\dfrac{1}{3}SD.\dfrac{1}{2}AD\left(AB+CD\right)=...\)
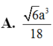
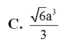
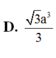

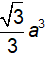
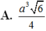
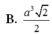
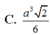
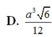

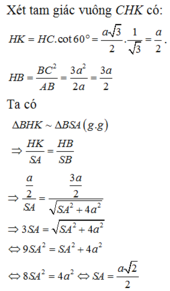
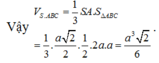
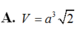
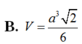
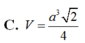
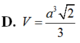



\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
\(\Rightarrow\widehat{DSA}\) là góc giữa SD và (SAB)
\(\Rightarrow\widehat{DSA}=60^0\)
\(\Rightarrow SA=\dfrac{AD}{tan60^0}=\dfrac{a\sqrt{3}}{3}\)
\(\Rightarrow V_{S.ABC}=\dfrac{1}{3}SA.\dfrac{1}{2}AB.AC=\dfrac{a^3\sqrt{3}}{18}\)
{SA⊥(ABCD)⇒SA⊥ADAD⊥AB \Rightarrow AD\perp\left(SAB\right)⇒AD⊥(SAB)
\Rightarrow\widehat{DSA}⇒DSA là góc giữa SD và (SAB)
\Rightarrow\widehat{DSA}=60^0⇒DSA=600
\Rightarrow SA=\dfrac{AD}{tan60^0}=\dfrac{a\sqrt{3}}{3}⇒SA=tan600AD=3a3
\Rightarrow V_{S.ABC}=\dfrac{1}{3}SA.\dfrac{1}{2}AB.AC=\dfrac{a^3\sqrt{3}}{18}⇒VS.ABC=31SA.21AB.AC=18a33