Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

AM là hình chiếu của SM trên (ABCD).
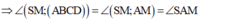
- Xét tam giác vuông ABM ta có: 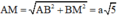
- Xét tam giác vuông SAM ta có: 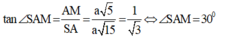


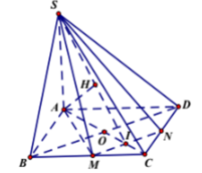
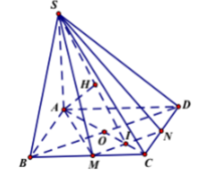
Dựng CH _|_ AB => CH _|_ (SAB)
Giả sử MN cắt AD tại F. Theo định lý Talet ta có:
\(\frac{DF}{MC}=\frac{ND}{NC}=\frac{1}{2}\Rightarrow DF=\frac{MC}{2}=\frac{a}{4}\)
Khi đó \(\frac{PA}{PC}=\frac{AF}{MC}=\frac{5}{2}\Rightarrow\frac{CA}{PA}=\frac{7}{5}\)
Do đó: d (P;(SAB))=\(\frac{5}{7}d\left(C;\left(SAB\right)\right)=\frac{5}{7}CH=\frac{5}{7}\cdot\frac{a\sqrt{3}}{2}=\frac{5a\sqrt{3}}{14}\)

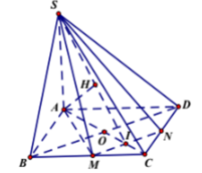
Gọi I = AC ∩ MN ⇒ I là trung điểm của OC, ta có:
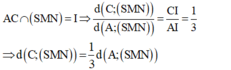
- Ta có: MN// BD mà BD ⊥ (SAC)(cmt) ⇒ MN ⊥ (SAC).
- Trong (SAC) kẻ AH ⊥ SI (H ∈ SI) ⇒ MN ⊥ AH.
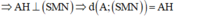
- Ta có:
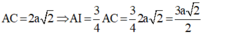
- Xét tam giác vuông SAI ta có:
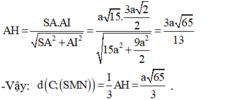

tham khảo
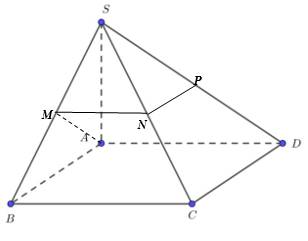
\(SA\perp\left(SBCD\right)\) nên \(SA\perp BC\)
Mà \(BC\perp AB\) nên \(BC\perp\left(SAB\right)\)
Tam giác \(SBC\) có \(MN\) là đường trung bình nên \(MN//BC,MN=\dfrac{1}{2}BC=\dfrac{a}{2}\text{}\)
Suy ra:\(MN\perp\left(SAB\right)\) và \(MN\perp AM\)
Tam giác \(SCD\) có \(NP\) là đường trung bình nên \(NP//CD\)
Mà \(MN//BC,BC\perp CD\)
Suy ra \(MN\perp NP\)
Vậy \(d\left(AM,NP\right)=MN=\dfrac{a}{2}\)