Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\text{Δ}ABC\sim\text{Δ}HBA;\text{Δ}ABC\sim\text{Δ}HCA\)
b: \(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{15\cdot20}{25}=12\left(cm\right)\)
\(BH=\dfrac{AB^2}{BC}=\dfrac{15^2}{25}=9\left(cm\right)\)
CH=BC-BH=25-9=16(cm)

Đáp án D
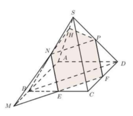
Phương pháp:
Qua M dựng các đường thẳng song song với BD và SC.
Cách giải:

Trong (SAB) kéo dài MN cắt SA tại H.
Vậy thiết diện của chóp khi cắt bởi mặt phẳng (P) là ngũ giác EFPHN.

gọi H, K là trung điểm AB, AC thì HK là đường tb của hình thang DMNE. HK=(DM+EN)/2
Bc=2HK

Đáp án D
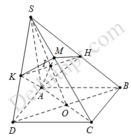
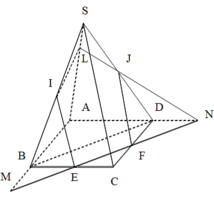
Gọi O là tâm của hình bình hành ABCD, nối S O ∩ A M = I .
Qua I kẻ đường thẳng d, song song với BD cắt SB, SD lần lượt tại H, K suy ra



Chọn đáp án D
Ta có
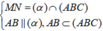
![]()
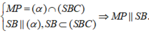
![]()
Khi đó ![]()
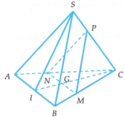
Gọi I là trung điểm của AB.
Ta có SA=SB=AB=CA=CB=a nên tam giác SAB và tam giác ABC đều cạnh a.
Khi đó A B ⊥ S I , A B ⊥ C I và S I = C I = a 3 a
![]()
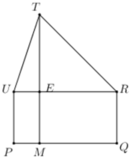
Mặt khác S I = C I = S C = a 3 2 nên ∆ S I C đều
![]()
Vậy góc giữa hai mặt phẳng (MNP) và (ABC) bằng 60 0
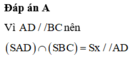
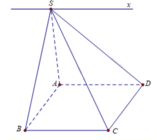




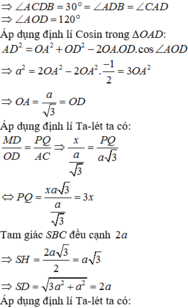
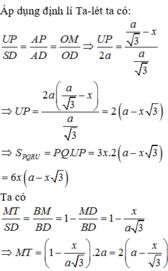
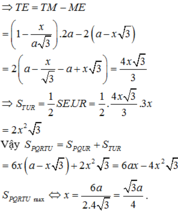
Đường thẳng đi qua S và song song với AB.
Đáp án B