Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
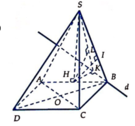
Vẽ đường thẳng d qua B và song song với AC.
Gọi K, I lần lượt là hình chiếu của H trên d và SB, L là hình chiếu của H trên SK.
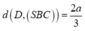
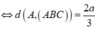
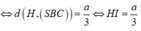
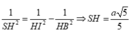
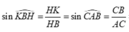
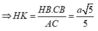
![]()
![]()
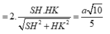

Chọn A

Gọi H là trung điểm của AC. Đỉnh S cách đều các điểm A, B, C
=> SH ⊥ (ABC)
Xác đinh được
![]()
Ta có MH // SA
![]()
Gọi I là trung điểm của AB => HI ⊥ AB
![]()
và chứng minh được HK ⊥ (SAB)
![]()
Trong tam giác vuông SHI tính được
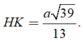

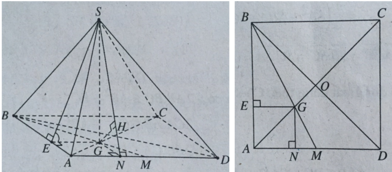
+ Xác định góc của (SAB) và mặt phẳng đáy.
Gọi G là trọng tâm tam giác ABD và E là hình chiếu của G lên AB. Ta có:
AB ⊥ SG & AB ⊥ GE⇒ AB ⊥ (SEG) ⇒ AB ⊥ SE.
SE ⊥ AB & GE ⊥ AB⇒ ∠((SAB),(ABCD)) = ∠(SEG) = 60o.
+ Xác định khoảng cách từ B đến mặt phẳng (SAD).
Hạ GN ⊥ AD. Tương tự như trên, ta có: AD ⊥ GN & AD ⊥ SG⇒ AD ⊥ (SGN)
Hạ GH ⊥ SN, ta có GH ⊥ (SAD) suy ra khoảng cách từ G đến (SAD) là GH.
+ Tính GH.
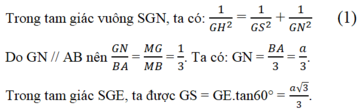
(do GE = GN). Thế vào (1) ta được:
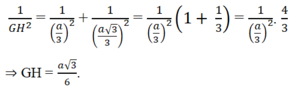
Ta có: M ∈(SAD) & MB = 3MG⇒ d(B,(SAD)) = 3d(G,(SAD)) = (a√3)/2.

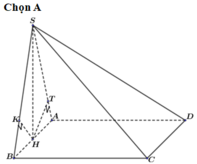
Chọn đáp án A
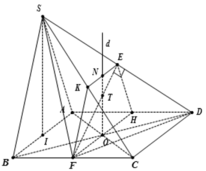
+ Gọi O là tâm của hình vuông ABCD. Qua O ta dựng đường thẳng d vuông góc với mặt đáy.
+ Gọi E, K, F, H, N lần lượt là trung điểm của các đoạn thẳng SD, SC, BC, AD, EK
+ Ta có tam giác SDF là tam giác cân tại F. Vì FD = FS = a 5 (độc giả tự chứng minh)
Suy ra FE ⊥ SD
Mặt khác, ta có KE // FH (Vì cùng song song với CD). Nên 4 điểm K, E, F, H đồng phẳng
+ Trong mặt phẳng (KEFH), gọi T là giao điểm của FE và ON.
Ta có T là tâm mặt cầu ngoại tiếp hình chóp S. ABCD
+ Ta có tam giác EKO là tam giác đều cạnh a. Nên
![]()
Bán kính mặt cầu là
![]()
+ Xét tam giác vuông TOB vuông tại B, ta có
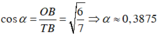

Đáp án B.
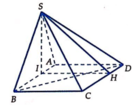
Ta có AD//BC, ![]() => AD//(SBC)
=> AD//(SBC)
=> d(AD;SC) = d(AD;(SBC)) = d(D;(SBC)).
Qua I kẻ đường thẳng song song với AD, cắt CD tại H.
Suy ra IH ⊥ CD
Từ CD ⊥ IH, CD ⊥ SI=> CD ⊥ (SIH)=> CD ⊥ SH
Suy ra ![]()
![]()
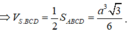
Lại có
![]()
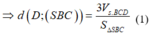
Từ ![]()
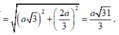
![]()
![]()
Suy ra
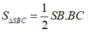
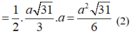
Từ (1) và (2), suy ra
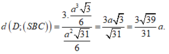
Vậy
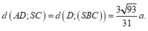
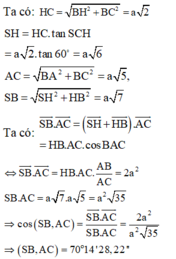


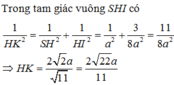

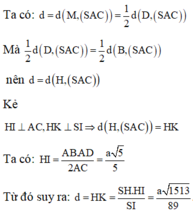

- Ta có: CD // AB nên CD// mp (SAB)
⇒ Suy ra:
- Kẻ MH ⊥ AB, HK ⊥ SM.
- Do đó, tam giác ABC là tam giác đều.
- Xét tam giác SHM vuông tại H; đường cao HK có: