Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi O là giao điểm của AC và BD.
ABCD là hình thoi ⇒ AC ⊥ BD,
Vì O là trung điểm của AC, BD nên:


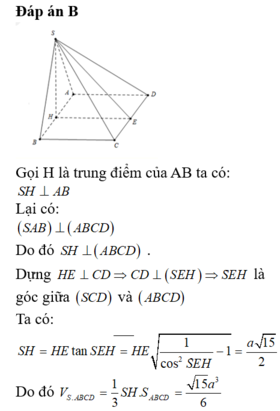
Đáp án B
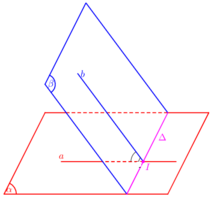
Phương pháp:
Xác định góc giữa hai mặt phẳng (α;β)
- Tìm giao tuyến Δ của (α;β)
- Xác định 1 mặt phẳng γ ⊥ Δ
- Tìm các giao tuyến a = α∩γ, b = β ∩ γ
- Góc giữa hai mặt phẳng (α;β):(α;β) = (a;b)
Cách giải:
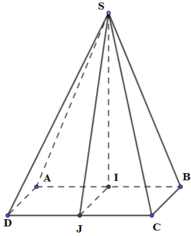
Gọi I, J lần lượt là trung điểm của AB, CD.
Tam giác SAB cân tại S ⇒ SI ⊥ AB
Vì mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD) nên SI ⊥ (ABCD)
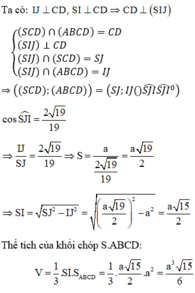

Chọn D
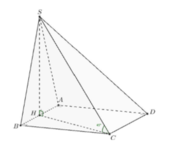
Gọi H là trung điểm của AB.
![]()
![]()
Do đó:
![]()
Xét tam giác vuông BHC:
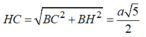
Xét tam giác vuông SHC:
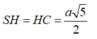
Suy ra:
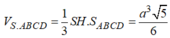

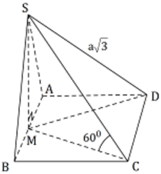
S B N M C D I K A
Gọi I là trung điểm của đoạn AB \(\Rightarrow SI\perp AB,\left(SAB\right)\perp\left(ABCD\right)\Rightarrow SI\perp\left(ABCD\right)\)
Nên \(\widehat{SCI}=\left(\widehat{SC,\left(ABCD\right)}\right)=60^0,CI=\frac{a\sqrt{3}}{2}\Rightarrow SI=CI\tan60^0=\frac{3a}{2}\)
Gọi M là trung điểm của đoạn BC, N là trung điểm đoạn BM
\(AM=\frac{a\sqrt{3}}{2}\Rightarrow IN=\frac{a\sqrt{3}}{4}\)
Ta có : \(S_{ABCD}=2S_{\Delta ABC}=\frac{a^2\sqrt{3}}{2}\Rightarrow V_{S.ABCD}=\frac{1}{3}.\frac{a^2\sqrt{3}}{2}.\frac{3a}{2}=\frac{a^2\sqrt{3}}{4}\)
Ta có \(BC\perp IN,BC\perp SI\Rightarrow BC\perp\left(SIN\right)\)
Trong mặt phẳng (SIN) kẻ \(IK\perp\left(SN\right),K\in SN\), ta có :
\(\begin{cases}IK\perp SN\\IK\perp BC\end{cases}\) \(\Rightarrow IK\perp\left(SBC\right)\Rightarrow d\left(I,\left(SBC\right)\right)=IK\)
Lại có :
\(\frac{1}{IK^2}=\frac{1}{IS^2}+\frac{1}{IN^2}\Rightarrow IK=\frac{3a\sqrt{13}}{26}\Rightarrow d\left(I,\left(SBC\right)\right)=\frac{3a\sqrt{13}}{26}\)
\(\Rightarrow d\left(A,\left(SBC\right)\right)=\frac{3a\sqrt{13}}{13}\)
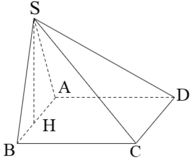

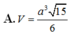
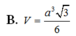
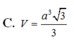
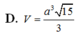

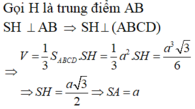
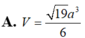
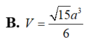
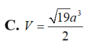
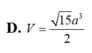
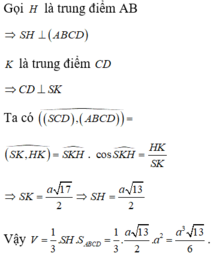
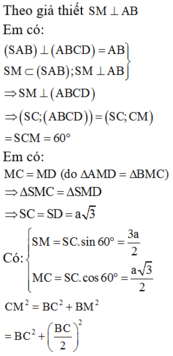
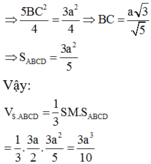
Lời giải:
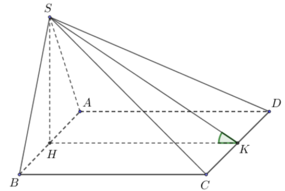
Kẻ \(SH\perp BA\)
Vì \((SAB)\perp (ABCD); (SAB)\cap (ABCD)=BA\) nên \(SH\perp (ABCD)\)
Từ dữ kiện đề bài:
\(S_{ABCD}=AC.BD=a\sqrt{3}.a=\sqrt{3}a^2\)
Gọi \(O=AC\cap BD\). Theo tính chất hình thoi:
\(AO=\frac{AC}{2}=\frac{\sqrt{3}a}{2}; BO=\frac{BD}{2}=\frac{a}{2}\)
\(\rightarrow AB=\sqrt{AO^2+BO^2}=a\)
Vì $SAB$ vuông cân tại $S$ nên \(SB=SA=\frac{AB}{\sqrt{2}}=\frac{a}{\sqrt{2}}\)
\(S_{SAB}=\frac{SA.SB}{2}=\frac{SH.AB}{2}\rightarrow SH=\frac{SA.SB}{AB}=\frac{\frac{a}{\sqrt{2}}.\frac{a}{\sqrt{2}}}{a}=\frac{a}{2}\)
Vậy:
\(V_{S.ABCD}=\frac{1}{3}SH.S_{ABCD}=\frac{1}{3}.\frac{a}{2}.\sqrt{3}a^2=\frac{\sqrt{3}a^3}{6}\)