Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Phương pháp:
- Dựng hình hộp chữ nhật SB'C'D'.ABCD, xác định góc giữa BD và (SBC) (nhỏ hơn 90 0 ) là góc giữa
BD và hình chiếu của nó trên (SBC) .
- Sử dụng các kiến thức hình học đã học ở lớp dưới tìm sin α .
Cách giải:
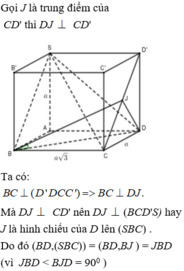
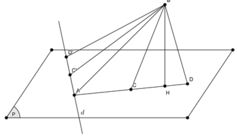
Qua B,C,D lần lượt kẻ các đường thẳng vuông góc với đáy.
Dựng hình hộp chữ nhật SB'C'D'.ABCD như hình vẽ.
Dễ thấy mặt phẳng (SBC) được mở rộng thành mặt phẳng (SBCD').
Tam giác D'DC có D'D = DC = a và D = 90 0 nên vuông cân tại D
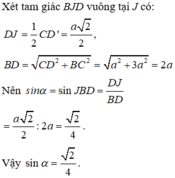

Chọn A.
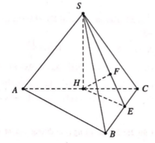
Dựng SH ⊥ AC , do ( SAC ) ⊥ ( ABC ) nên SH ⊥ ( ABC ) ; AC = 2 a . Dựng HE ⊥ BC ; HF ⊥ SE ⇒ d ( H ; ( SBC ) ) = HF . ΔSAC = ΔBCA ⇒ ΔSAC vuông tại S .
Dễ thấy tan ACB ^ = 1 3 ⇒ ACB ^ = 30 o = SAC ^ HC = SCcos 60 o = a 2 ; HE = HCsin 30 o = a 4 ; SH = a 3 2 . Do AC = 4 HC ⇒ d A = 4 d H = 4 . SH . HE SH 2 + HE 2 = 2 39 13 Do đó Sinα = d A SA = 2 13 .

Đáp án C
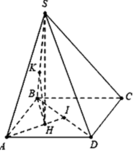
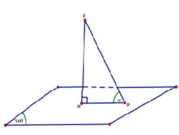
Gọi H là tâm đường tròn ngoại tiếp đều ∆ABD
Ta có 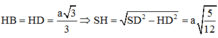
Lại có d(H;(SBC)) = HK và 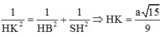
Khoảng cách từ D →(SBC) là 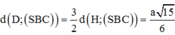
Vậy ∆ABD ![]()
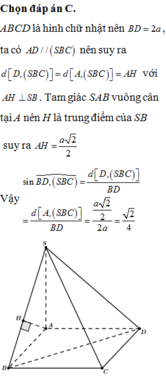




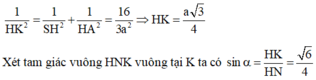

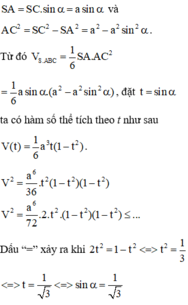



Đáp án C
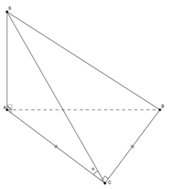
Dựng hình bình hành SBCM. Kẻ D H ⊥ C M H ∈ C M
Ta có
B D ⊥ S B C = B D H ⊥ S B C ⇒ B D ; S B C ^ = B D ; B H ^ = D B H ^ = α
Tam giác CDM vuông cân tại D, có C D = a ⇒ D H = a 2 2
Tam giác BDH vuông tại H, có sin α = D H B D = 2 4 .