Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: SA\(\perp\)(ABC)
=>SA\(\perp\)AB; SA\(\perp\)AC; SA\(\perp\)BC
=>ΔSAB vuông tại A và ΔSAC vuông tại A
Ta có: ΔABC vuông cân tại B
=>BA=BC=a và \(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\widehat{SA;AB}=\widehat{SAB}=90^0\)
b: \(\widehat{SB;BA}=\widehat{SBA}\)
Xét ΔSAB vuông tại A có \(tanSBA=\dfrac{SA}{AB}=\dfrac{a\sqrt{2}}{a}=\sqrt{2}\)
nên \(\widehat{SBA}\simeq54^044'\)
=>\(\widehat{SB;BA}\simeq54^044'\)
Chú ý :
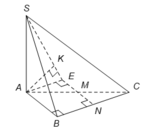
Nếu kẻ KI // AD và kẻ IJ // CK thì IJ là đoạn vuông góc chung của SA và BC
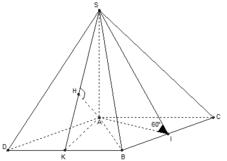
+) Hình chiếu vuông góc của SI trên mặt phẳng (ABC) là AI nên góc giữa SI và mặt phẳng (ABC) là:
(vì tam giác SIA vuông tại A nên góc SIA nhọn) ⇒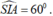 
+) Xét tam giác SIA vuông tại A,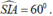 
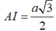nên:
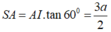
+) Dựng hình bình hành ACBD, tam giác ABC đều nên tam giác ABD đều.
+) Ta có:
AC // BD; BD ⊂ (SBD) nên AC // (SBD).
mà SB ⊂ (SBD) nên d(AC, SB) = d(A, (SBD)).
- Gọi K là trung điểm đoạn BD, tam giác ABD đều suy ra AK ⊥ BD và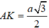 
mà BD ⊥ SA nên BD ⊥ (SAK).
- Dựng AH ⊥ SK; H ∈ SK.
- Lại có AH ⊥ BD suy ra AH ⊥ (SBD).
- Vậy d(A, (SBD)) = AH.
- Xét tam giác SAK vuông tại vuông tại A, đường cao AH ta có:
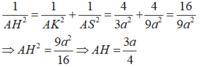
- Vậy d(AC, SB) = d(A, (SBD))
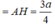
Chọn D
Xác định được
Gọi N là trung điểm BC, suy ra MN//AB.
Lấy điểm E đối xứng với N qua M, suy ra ABNE là hình chữ nhật.
Do đó
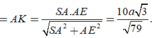
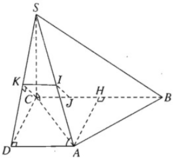
a) Gọi H là trung điểm của đoạn BC. Qua A vẽ AD song song với BC và bằng đoạn HC thì góc giữa BC và SA là góc ∠SAD. Theo định lí ba đường vuông góc, ta có SD ⊥ DA và khi đó:
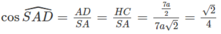
Vậy góc giữa BC và SA được xác định sao cho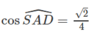 
Vì BC // AD nên BC song song với mặt phẳng (SAD). Do đó khoảng cách giữa SA và BC chính là khoảng cách từ đường thẳng BC đến mặt phẳng (SAD).
Ta kẻ CK ⊥ SD, suy ra CK ⊥ (SAD), do đó CK chính là khoảng cách nói trên. Xét tam giác vuông SCD với đường cao CK xuất phát từ đỉnh góc vuông C ta có hệ thức:
Chú ý. Nếu kẻ KI // AD và kẻ IJ // CK thì IJ là đoạn vuông góc chung của SA và BC.
Do SA ⊥ (ABCD) ⇒ \(\left\{{}\begin{matrix}SA\perp AB\\SA\perp AC\\SA\perp BC\end{matrix}\right.\)
Mà BC ⊥ AC ⇒ BC ⊥ (SAC) ⇒ BC ⊥ SC và BC ⊥ AH
Do BC ⊥ AH và AH ⊥ SC ⇒ AH ⊥ (SBC) ⇒ AH ⊥ KH ⇒ \(\widehat{AHK}=90^0\)
ΔSAB và ΔSAC vuông tại A
Mà AH và AK lần lượt là đường cao của ΔSAB và ΔSAC
⇒ \(\left\{{}\begin{matrix}SA^2=SK.SB\\SA^2=SH.SC\end{matrix}\right.\)
⇒ SK . SB = SH . SC
⇒ \(\dfrac{SK}{SH}=\dfrac{SC}{SB}\) ⇒ ΔSKH \(\sim\) ΔSCB ⇒ \(\widehat{SKH}=\widehat{SCB}=90^0\)
⇒ HK ⊥ SB
Mà AK⊥ SB
⇒ ((SAB),(SCB)) = (AK,AH) = \(\widehat{KAH}\) = 450 (đây là góc nhọn, vì \(\widehat{AHK}=90^0\))
⇒ ΔHAK vuông cân tại H ⇒ AK = \(\sqrt{2}AH\)
Ta có : \(\dfrac{S_{SAC}}{S_{SAB}}=\dfrac{\dfrac{1}{2}.AH.SC}{\dfrac{1}{2}AK.SB}=\dfrac{\dfrac{1}{2}.SA.AC}{\dfrac{1}{2}.SA.AB}\)
⇒ \(\dfrac{AH.SC}{AK.SB}=\dfrac{SA.AC}{SA.AB}\)
⇒ \(\dfrac{1}{\sqrt{2}}\) . \(\dfrac{SC}{SB}\) = \(\dfrac{AC}{AB}\). Mà AC = a và AB = 2a
⇒ \(\dfrac{1}{\sqrt{2}}\)\(\dfrac{SC}{SB}\) = \(\dfrac{1}{2}\) ⇒ \(\dfrac{SC^2}{SB^2}\) = \(\dfrac{1}{2}\) . Mà SB2 - SC2 = BC2 = 3a2
⇒ \(\left\{{}\begin{matrix}SC^2=3a^2\\SB^2=6a^2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}SB=a\sqrt{6}\\SC=a\sqrt{3}\end{matrix}\right.\) ⇒ SA = a\(\sqrt{2}\)
Từ đó ta tính được SH = \(\dfrac{2a\sqrt{3}}{3}\) và SK = \(\dfrac{a\sqrt{6}}{3}\)
Gọi M là trung điểm của SB thì ta có CM // HK (cùng vuông góc với SB)
Khoảng cách từ HK đến AC bằng khoảng cách từ HK đến (AMC)
a: BC vuông góc AM
BC vuông góc SA
=>BC vuông góc (SAM)
b: BC vuông góc (SAM)
=>BC vuông góc SM
=>(SM;(ABC))=90 độ
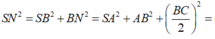
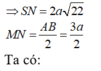
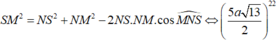
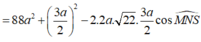
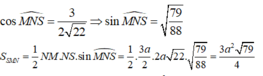
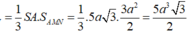
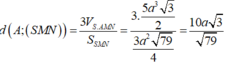
a: \(\widehat{SB;AB}=\widehat{SBA}\)
SA\(\perp\)(ABC)
=>\(SA\perp AB;SA\perp AC;SA\perp BC\)
Xét ΔSAB vuông tại A có \(tanSBA=\dfrac{SA}{AB}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
=>\(\widehat{SBA}=60^0\)
=>\(\widehat{SB;AB}=60^0\)
b:
\(\widehat{SC;AC}=\widehat{SCA}\)
Xét ΔSAC vuông tại A có \(tanSCA=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
nên \(\widehat{SCA}=60^0\)
=>\(\widehat{SC;AC}=60^0\)
c: ΔABC đều có AM là đường trung tuyến
nên \(AM=BC\cdot\dfrac{\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\)
Ta có: SA\(\perp\)(ABC)
AM\(\subset\)(ABC)
Do đó: SA\(\perp\)AM
=>ΔSAM vuông tại A
\(\widehat{SM;AM}=\widehat{SMA}\)
Xét ΔSMA vuông tại A có \(tanSMA=\dfrac{SA}{AM}=\dfrac{a\sqrt{3}}{\dfrac{a\sqrt{3}}{2}}=2\)
=>\(\widehat{SMA}\simeq63^026'\)
=>\(\widehat{SM;AM}\simeq63^026'\)
a.
Góc giữa SB và AB là góc \(\widehat{SBA}\)
Trong tam giác vuông SAB:
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
\(\Rightarrow\widehat{SBA}=60^0\)
b.
Góc giữa SC và AC là góc \(\widehat{SCA}\)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=\sqrt{3}\Rightarrow\widehat{SCA}=60^0\)
c.
Góc giữa SM và AM là góc \(\widehat{SMA}\)
AM là trung tuyến tam giác đều \(\Rightarrow AM=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow tan\widehat{SMA}=\dfrac{AM}{SA}=2\Rightarrow\widehat{SMA}=60^026'\)