Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: B
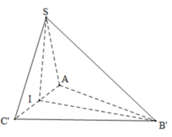
Trên SB, SC lần lượt lấy các điểm B',C' sao cho SB' =SC' =3.
Khi đó S.AB'C' là tứ diện đều (cạnh bằng 3).
Ta có V S . A B ' C ' = 9 2 4 = V 1
⇒ V S . A B C = 6 3 . 9 3 . V 1 = 27 2 2
S ∆ S A B = 1 2 . 3 . 6 . sin 60 o = 9 3 2
d ( C , ( S A B ) ) = 3 . V S . A B C S ∆ A B C = 3 6

Chọn đáp án B.
Ta có: S A ⊥ S B S A ⊥ S C ⇒ S A ⊥ ( S B C )
Vì vậy áp dụng công thức cho trường hợp khối chóp có cạnh bên vuông góc đáy có:
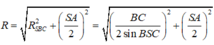
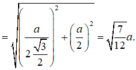
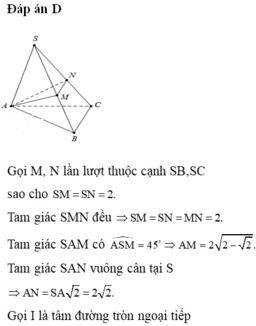

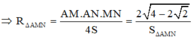
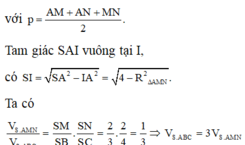
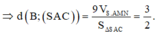
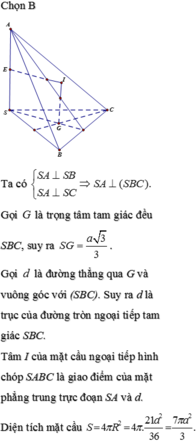


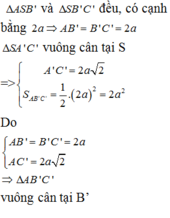


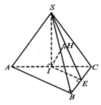
Chọn điểm B' và C' lần lượt thuộc SB và SC sao ctho SA=SB'=SC'=3
Thấy ngay các tam giác SAB', SB'C', SAC', AB'C' đều
suy ra tứ diện SAB'C' là tứ diện đều, cạnh bằng 3
Dễ dàng tính được \(V_{SAB'C'}=\frac{9\sqrt{2}}{4}\)
Dùng tỷ lệ thể tích: \(\frac{V_{S.ABC}}{V_{S.AB'C'}}=\frac{SA}{SA}\cdot\frac{SB}{SB'}\cdot\frac{SC}{SC'}=1\cdot\frac{6}{3}\cdot\frac{9}{3}=6\Rightarrow V_{S.ABC}=\frac{27\sqrt{3}}{2}\)
\(S_{SAB}=\frac{1}{2}.SA.SB.sin\widehat{ASB}=\frac{9\sqrt{3}}{2}\)
\(\Rightarrow d\left(C;\left(SAB\right)\right)=\frac{3V_{S.ABC}}{S_{SAB}}=9\)
nếu tính như vậy thì thể tích S.ABC=\(\frac{27\sqrt{2}}{2}\) chứ ạ?