Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dễ dàng chứng minh MN // BC
Xét \(\Delta SBC\) có MN // BC và MN đi qua trọng tâm G
\(\Rightarrow\) \(\begin{cases}SM=\frac{2}{3}SB\\SN=\frac{2}{3}SC\end{cases}\)
Sử dụng công thức tỉ lệ thể tích đố với 2 khối tứ diện S.AMN và S.ABC ta có
\(\frac{V_{S.AMN}}{V_{S.ABC}}=\frac{SA}{SA}.\frac{SM}{SB}.\frac{SN}{SC}=1.\frac{2}{3}.\frac{2}{3}=\frac{4}{9}\\ \Rightarrow V_{S.AMN}=\frac{4}{9}.V_{S.ABC}\)
Tính được \(V_{S.ABC}=\frac{1}{6}SA.AB.BC=\frac{a^3}{6}\)
\(\Rightarrow V_{S.AMN}=\frac{2a^3}{27}\)

Chọn D.
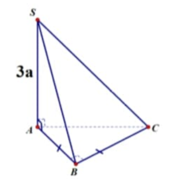
Góc giữa mặt phẳng (ABC) và góc S B A ^ = 60 o .
Xét tam giác SAB vuông tạ A có SA=3a, S B A ^ = 60 o nên A B = S A tan 60 o = a 3 .
Khi đó S A B C = 1 2 B A . B C = 3 a 2 2 nên
V S . A B C = 1 3 S A . S A B C = 3 a 3 2


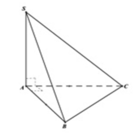


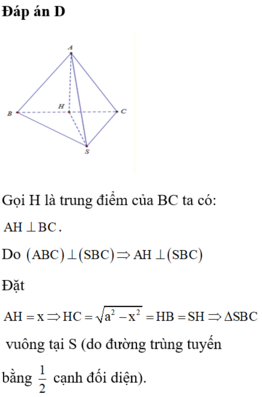

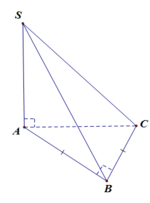
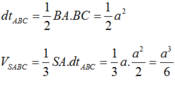

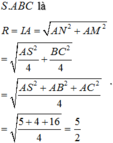
\(AB=BC=\frac{AC}{\sqrt{2}}=a\)
\(\Rightarrow V=\frac{1}{3}SA.\frac{1}{2}AB.BC=\frac{a^3\sqrt{3}}{6}\)