Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
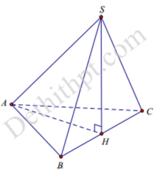
Vì hai tam giác ABC và SBC đều và có chung cạnh BC nên bằng nhau ⇒ A H = S H .
Mà Δ H S A vuông tại H nên vuông cân
⇒ S A H ^ = 45 °

Đáp án là D
Gọi H là trung điểm B C . Ta có A H là hình chiếu vuông góc của S A lên mặt phẳng A B C .
Khi đó S A ; A B C ^ = S A ; A H ^ = S A H ^
Ta có S H = A H S H ⊥ A H ⇒ Δ S A H vuông cân tại - H ⇒ S A H ^ = 45 0 .

Đáp án D
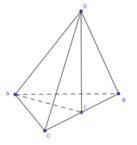
Góc giữa cạnh SA và đáy là SAF ,
Vì tam giác ABC và SBC là tam giác đều cạnh a nên ta có
A F = 3 2 a ; S F = 3 2 a
Vậy tan S A F ^ = 1 ⇒ S A G ^ = 45 0

Đáp án A.
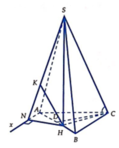
Ta có S C H ^ = 60 ° và
H C = a 7 3 ; S H = H C tan S C H ^ = a 21 3
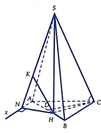
Từ A kẻ tia A x / / C B (như hình vẽ). Khi đó B C / / S A x và do B A = 3 2 H A nên
d B C , S A = d B C , S A x = d B , S A x = 3 2 d H , S A x
Gọi N và K lần lượt là hình chiếu vuông góc của H trên Ax và SN.
Do A N ⊥ S H N và H K ⊥ S N nên H K ⊥ S A N . Khi đó d B C , S A = 3 2 H K .
Ta có
A H = 2 a 3 ; H N = A H sin N A H ^ = a 3 3 .
Suy ra H K = H N . H S H N 2 + H S 2 = a 42 12 . Vậy d B C , S A = a 42 8 .

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2
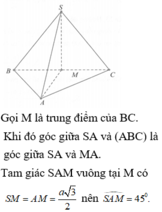




Đáp án D
Ta có H là trung điểm của BC, H là hình chiếu của S trên mặt phẳng (ABC) nên HA là hình chiếu của SA trên mặt phẳng (ABC).
Suy ra S A , A B C ^ = S A , H A ^ = S A H ^ .
Lại có Δ A B C = Δ S B C (đều là các tam giác đều cạnh a) nên A H = S H ⇒ Δ S H A vuông cân tại H.
Vậy S A , A B C ^ = S A H ^ = 45 ° .