Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
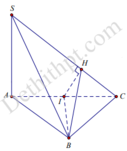
Vì Δ A B C cân tại B nên I là trung điểm của AC nên B I ⊥ A C .
Ta có:
S A ⊥ B I , B I ⊥ A C ⇒ B I ⊥ S A C ⇒ B I ⊥ S C
mà
S C ⊥ I H ⇒ S C ⊥ B I H ⇒ S B C ⊥ B I H .

Đáp án A
Phương pháp:
Gọi M là trung điểm của AB, chứng minh S M ⊥ A B C bằng cách sử dụng tính chất của trục đường tròn đáy.
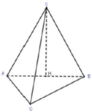
Cách giải: Gọi M là trung điểm của AB.
Vì Δ A B C vuông tại C nên M A = M B = M C . .
Mà S A = S B = S C nên SM là trục đường tròn ngoại tiếp tam giác ABC.
Suy ra S M ⊥ A B C .
Vậy H ≡ M là trung điểm của AB.
Chú ý khi giải: Cần tránh nhầm lẫn với trường hợp chóp tam giác đều: HS dễ nhầm lẫn khi nghĩ rằng S A = S B = S C thì hình chiếu vuông góc của S sẽ là trọng tâm tam giác dẫn đến chọn nhầm đáp án B.

a d e m n b c i h
a, tam giác ade cân a
=> góc d = góc e và ad = ae
tam giác adb = tam giác aec ( cgc)
=> ab=ac
=> tam giác abc cân a
b, tam giác bmd vuông m và tam giác cne vuông n
góc m = góc n =90 độ
góc d = góc e
bd = ce
=> bmd = cne (ch-gn)
=> bm = cn
c, có tam giác bmd = tam giác cne
=> góc mbd = góc nce
mà góc cbi đối đỉnh góc mbd, bci đối đỉnh nce
=> góc cbi = góc bci
=> tam giác ibc cân i
d, lây h là trung điểm bc
tam giác abc cân a có ah là đường trung tuyến úng với bc
=> ah vừa là trung tuyến vừa là đường cao ứng với bc
cmtt với ibc => ih vừa là trung tuyến vừa là đường cao ứng với bc
=> a,i,h thẳng hàng
=> ai vừa trung tuyến vừa là đường cao tam giác abc cân a
=> đpcm

Đáp án A
Gọi M là trung điểm của AC. Tam giác ABC vuông tại B, do đó M là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi O là trung điểm của AC, suy ra OM // SA. Mà

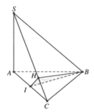


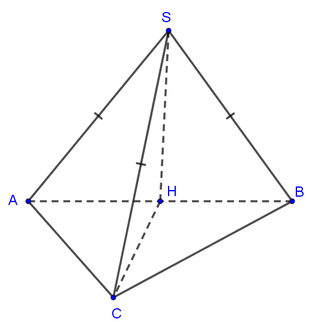

Chọn B