K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

QD
24 tháng 4 2017
a) Diện tích đáy của hình chóp đều:
S = BC 2 = 6,52 = 42,25 (m2)
Thể tích hình chóp đều:
V = \(\dfrac{1}{3}\). S.h = \(\dfrac{1}{3}\). 42,25 . 12 ≈ 169 (cm3)
b) Các mặt xung quanh là những hình thang cân đáy nhỏ 2cm, đáy lớn 4cm, chiều cao 3,5cm. Nên:
Sxq = \(4.\dfrac{\left(2+4\right).3,5}{2}=42\left(cm^2\right)\) = 42 (cm2)
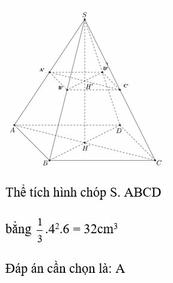

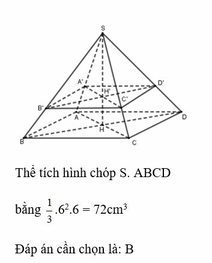




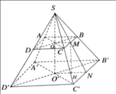


a) Gọi O là tâm của đáy ABCD, M là giao điểm của SO và mặt phẳng (P). Ta có: OM = 2(cm).
Ta tính được O B = 2 2 c m rồi suy ra SO = 5 (cm)
Từ đó chiều cao cần tìm là: SM = SO - OM 3 (cm)
b) Gọi I là trung điểm của BC. E, F, J lần lượt là giao điểm của SB, SC, SI với mặt phẳng (p).