Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

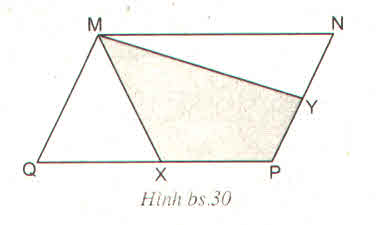
Kẻ đường chéo MP
Ta được SMQX= SMPX
SMNY=SMPY
=> SMXPY= SMPX + SMPY
Khi đó \(S_{MXPY}=\dfrac{1}{2}S\)
Nhớ tick nhé !
Sau khi kẻ đường thẳng MP ta có:
\(\Delta MPQ=\Delta MPN\) (cạnh-cạnh-cạnh)
=> \(\dfrac{1}{2}\)SMPQ = \(\dfrac{1}{2}S_{MPN}\)
hay \(\Delta MPX=\Delta MPY\).
Vì \(S_{MPX}+S_{MPY}=S_{MXPY}=S_{MXQ}+S_{MYN}\) nên SMXPY = \(\dfrac{1}{2}S\).
Vậy SMXPY = \(\dfrac{1}{2}S\).

* Phương án đúng:
(D). S
* Giải thích:
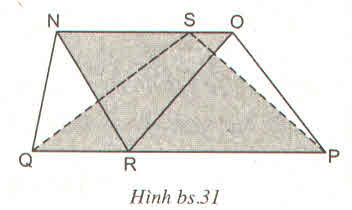
Đường cao của hình thang cũng chính bằng độ dài đường cao của hai tam giác QSP và NRO.
Gọi độ dài đường cao là h (h>0)
SQSP= \(\dfrac{1}{2}.h.QP\)
SNRO= \(\dfrac{1}{2}.h.NO\)
SNRO+SQSP=\(\dfrac{1}{2}.h.NO\)+\(\dfrac{1}{2}.h.QP\)= \(\dfrac{1}{2}.h.\left(NO+QP\right)\) (1)
Ta có:
SNOPQ=S=\(\left(NO+QP\right).h.\dfrac{1}{2}\) (2)
Từ (1) và (2) => SNRO+SQSP=S=\(\dfrac{1}{2}.h.\left(NO+QP\right)\)

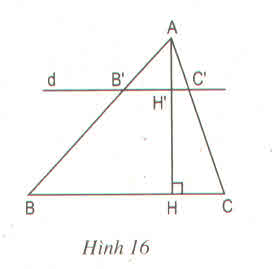
a) Chứng minh AH′AHAH′AH = B′C′BCB′C′BC
Vì B'C' // với BC => B′C′BCB′C′BC = AB′ABAB′AB (1)
Trong ∆ABH có BH' // BH => AH′AHAH′AH = AB′BCAB′BC (2)
Từ 1 và 2 => B′C′BCB′C′BC = AH′AHAH′AH
b) B'C' // BC mà AH ⊥ BC nên AH' ⊥ B'C' hay AH' là đường cao của tam giác AB'C'.
Áp dụng kết quả câu a) ta có: AH' =
a) Chứng minh AH′AHAH′AH = B′C′BCB′C′BC
Vì B'C' // với BC => B′C′BCB′C′BC = AB′ABAB′AB (1)
Trong ∆ABH có BH' // BH => AH′AHAH′AH = AB′BCAB′BC (2)
Từ 1 và 2 => B′C′BCB′C′BC = AH′AHAH′AH
b) B'C' // BC mà AH ⊥ BC nên AH' ⊥ B'C' hay AH' là đường cao của tam giác AB'C'.
Áp dụng kết quả câu a) ta có: AH' = 1313 AH
B′C′BCB′C′BC = AH′AHAH′AH = 1313 => B'C' = 1313 BC
=> SAB’C’= 1212 AH'.B'C' = 1212.1313AH.1313BC
=>SAB’C’= (1212AH.BC)1919
mà SABC= 1212AH.BC = 67,5 cm2
Vậy SAB’C’= 1919.67,5= 7,5 cm2

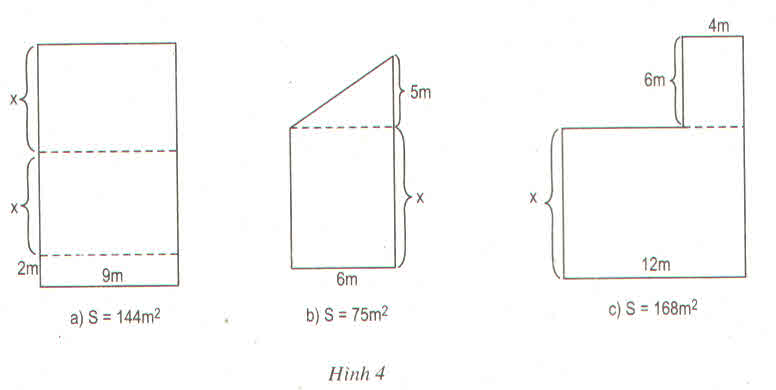
a) 9(2x+2)=144
18x +18=144
18x = 126
x = 7
Vậy x = 7m
b) 6x+15 = 75
6x = 60
x = 10
Vậy x = 10m
c) 12x+24 = 168
12x = 144
x =12
Vậy x = 12m.

Chia đám đất ABCDE thành hình thang ABCE và tam giác ECD. Cần vẽ đường cao CH của hình thang và đường cao DK của tam giác. Thực hiện các phép đo chính xác đến mm ta được AB = 30mm, CE = 26mm, CH = 13mm, DK = 7mm.
Nên SABCE = \(\dfrac{\text{(AB+EC).CH}}{2}\) = \(\dfrac{\text{(30+26).13 }}{2}\)=364 (mm2)
SECD = \(\dfrac{1}{2}\) EC. DK = \(\dfrac{1}{2}\)267= 91 (mm2)
Do đó SABCDE = SABCE + SECD = 364 + 91 = 455 (mm2)
Vì bản đồ được vẽ với tỉ lệ xích \(\dfrac{1}{5000}\) nên diện tích đám đất là:
S = 455. 5000 = 2275000 (mm2) = 2,275 (m2)

Hướng dẫn giải:
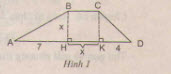
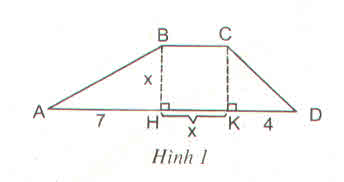
Gọi S là diện tích hình thang ABCD.
1) Theo công thức
S = BH(BC+DA)2BH(BC+DA)2
Ta có: AD = AH + HK + KD
=> AD = 7 + x + 4 = 11 + x
Do đó: S = x(11+2x)2x(11+2x)2
2) Ta có: S = SABH + SBCKH + SCKD.
= 1212.AH.BH + BH.HK + 1212CK.KD
= 1212.7x + x.x + 1212x.4
= 7272x + x2 + 2x
Vậy S = 20 ta có hai phương trình:
x(11+2x)2x(11+2x)2 = 20 (1)
7272x + x2 + 2x = 20 (2)
Cả hai phương trình không có phương trình nào là phương trình bậc nhất.
a) theo cách tính thứ nhất, diện tích hình thang là :
SABCD= BH.(BC+AD):2= x(x+7+x+4):2
=x(2x+11):2 = \(\dfrac{1}{2}\)x(2x+11) (đvdt) (1)
b) theo cách tính thứ hai
SABCD=SAHB+SCKD= \(\dfrac{1}{2}\).7x+x2+\(\dfrac{1}{2}\).4x
=\(\dfrac{7x+2x^2+4x}{2}\)= \(\dfrac{2x^2+11x}{2}\) (đvdt) (2)
Với S = 20 thì (1) và (2) trở thành x2+5,5x =20 thì đây là một phương trình bậc hai (vì có x2).
Vậy trong hai phương trình trên không có phương trình nào là phương trình bậc nhất.

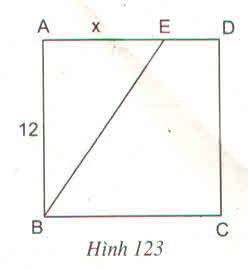
 AB.AE =
AB.AE =  hay 6x =
hay 6x = 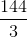
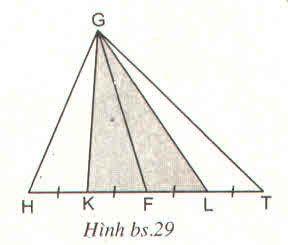
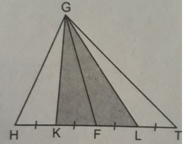
Vì SGKF=\(\dfrac{1}{2}.S_{GHF}\) (1)
SGFL= \(\dfrac{1}{2}.S_{GFT}\) (2)
Cộng (1) và (2) vế theo vế:
=> SGKL=\(\dfrac{1}{2}.\left(S_{GHF}+S_{GFT}\right)=\dfrac{1}{2}.S_{GTH}=\dfrac{1}{2}S\)
Nhớ tick nhé ,thank nhiều