Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định lí về đường trung tuyến:
OA2 = -
(1)
Thay OA = , AB = a, AD = BC = b và BD = m vào (1) ta có:
\(\left(\dfrac{n}{2}\right)^2=\dfrac{b^2+a^2}{2}-\dfrac{m^2}{4}\)
\(\Leftrightarrow\dfrac{n^2}{4}+\dfrac{m^2}{4}=\dfrac{a^2+b^2}{2}\)
\(\Leftrightarrow m^2+n^2=2\left(a^2+b^2\right)\)
A B C D a b n m

ta có \(\hept{\begin{cases}\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}\Rightarrow AC^2=AB^2+BC^2+2\overrightarrow{AB}.\overrightarrow{BC}\\\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{AD}\Rightarrow BD^2=BA^2+AD^2+2\overrightarrow{BA}.\overrightarrow{AD}\end{cases}}\)
mà \(\overrightarrow{AB}.\overrightarrow{BC}+\overrightarrow{BA}.\overrightarrow{AD}=\overrightarrow{AB}.\overrightarrow{BC}+\overrightarrow{AB}.\overrightarrow{AD}=0\)
Do đó \(AC^2+BD^2=2AB^2+2BC^2\Leftrightarrow m^2+n^2=2\left(a^2+b^2\right)\)

Áp dụng định lí về đường trung tuyến:
OA2 = –
Thay OA = , AB = a
AD = BC = b và BD = m => dpcm

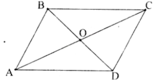
Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD.
Xét ΔABC có BO là trung tuyến
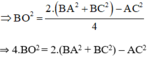
Mà O là trung điểm của BD nên BD = 2. BO ⇒ BD2 = 4. BO2
⇒ BD2 = 2.(AB2 + BC2) – AC2
⇒ BD2 + AC2 = 2.(AB2 + BC2)
⇒ m2 + n2 = 2.(a2 + b2) (ĐPCM).

Dễ dàng c/m : \(\dfrac{1}{a+2}+\dfrac{1}{b+2}+\dfrac{1}{c+2}=1\)
Ta có : \(\dfrac{1}{\sqrt{2\left(a^2+b^2\right)}+4}\le\dfrac{1}{a+b+4}\le\dfrac{1}{4}\left(\dfrac{1}{a+2}+\dfrac{1}{b+2}\right)\)
Suy ra : \(\Sigma\dfrac{1}{\sqrt{2\left(a^2+b^2\right)}+4}\le2.\dfrac{1}{4}\left(\dfrac{1}{a+2}+\dfrac{1}{b+2}+\dfrac{1}{c+2}\right)=\dfrac{1}{2}.1=\dfrac{1}{2}\)
" = " \(\Leftrightarrow a=b=c=1\)

Lời giải:
\(AC^2+BD^2=(\overrightarrow{AC})^2+(\overrightarrow{BD})^2\)
\(=(\overrightarrow{AB}+\overrightarrow{AD})^2+(\overrightarrow{BA}+\overrightarrow{BC})^2\)
\(=AB^2+AD^2+AB^2+BC^2+2\overrightarrow{AB}.\overrightarrow{AD}+2\overrightarrow{BA}.\overrightarrow{BC}\)
\(=2(a^2+b^2)+2\overrightarrow{AB}.\overrightarrow{AD}-2\overrightarrow{AB}.\overrightarrow{AD}=2(a^2+b^2)\)

a) Áp dụng định lí cosin ta có:
\(\left\{ \begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos ABC\\B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos BAD\end{array} \right.\)
Mà \(AD = BC;\cos BAD = \cos ({180^ \circ } - ABC) = - \cos ABC\)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}A{C^2} = A{B^2} + B{C^2} + 2.AB.BC.\cos BAD\\B{D^2} = A{B^2} + B{C^2} - 2.AB.AD.\cos BAD\end{array} \right.\end{array}\)
Cộng vế với vế ta được:
\( A{C^2} + B{D^2} = 2\left( {A{B^2} + B{C^2}} \right)\)
b) Theo câu a, ta suy ra: \(A{C^2} = 2\left( {A{B^2} + B{C^2}} \right) - B{D^2}\)
\(\begin{array}{l} \Rightarrow A{C^2} = 2\left( {{4^2} + {5^2}} \right) - {7^2} = 33\\ \Rightarrow AC = \sqrt {33} \end{array}\)