
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

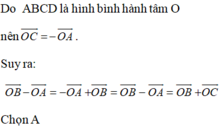

Bằng \(\overrightarrow{AB}\) là \(\overrightarrow{DC}\)
Bằng \(\overrightarrow{OB}\) là \(\overrightarrow{DO}\)
Có độ dài bằng OB là \(\overrightarrow{OB};\overrightarrow{BO};\overrightarrow{OD};\overrightarrow{DO}\)
a) Bằng vectơ AB :
\(\overrightarrow{DC}\)
Bằng vectơ OB :
\(\overrightarrow{DO}\)
b)Có độ dài bằng OB :
\(\overrightarrow{OD},
\overrightarrow{DO},
\overrightarrow{BO}\)

1. Kẻ đường kính chứa 1 trong 3 điểm A,B,C bất kỳ của (O)
Tam giác ABC chứa tâm O <=>
(*) Có nhiều nhất 2 điểm nằm
trên nửa đường tròn (O) có đường kính như trên , không nhận
cạnh nào là đường kính
(*) ABC là tam giác vuông
Nhận thấy khi tam giác ABC nội tiếp (O) thì A,B,C có 3 trường hợp:
TH1 : 3 điểm cùng nằm trên nửa (O ; DE/2) , không có cạnh nào là đường kính
TH2 : 2 điểm nằm trên nửa (O ; DE/2) ; 1 điểm trên nửa (O) còn lại
TH3 : Tam giác vuông
Biến cố A : " Tam giác ABC chứa tâm O"
=> P(A) = \(\dfrac{2}{3}\)

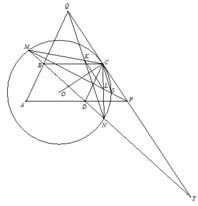
1). Gọi MN giao PQ tại T. Theo định lí Thales, ta có T P T C = T D T B = T C T Q .
Từ đó T C 2 = T P . T Q .
Do TC là tiếp tuyến của (O), nên T C 2 = T M . T N .
Từ đó T M . T N = T C 2 = T P . T Q , suy ra tứ giác MNPQ nội tiếp.

\(\overrightarrow{u}\overrightarrow{v}=0\Rightarrow\left(\overrightarrow{a}+3\overrightarrow{b}\right)\left(7\overrightarrow{a}-5\overrightarrow{b}\right)=7a^2+16\overrightarrow{a}\overrightarrow{b}-15b^2=0\left(1\right)\)
\(\overrightarrow{x}\overrightarrow{y}=0\Rightarrow\left(\overrightarrow{a}-4\overrightarrow{b}\right)\left(7\overrightarrow{a}-2\overrightarrow{b}\right)=7a^2-30\overrightarrow{a}\overrightarrow{b}+8b^2=0\left(2\right)\)
(1) và (2): \(\left\{{}\begin{matrix}7a^2+16\overrightarrow{a}\overrightarrow{b}-15b^2=0\\7a^2-30\overrightarrow{a}\overrightarrow{b}+8b^2=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{a}\overrightarrow{b}=\frac{b^2}{2}\\a^2=b^2\Rightarrow\left|a\right|=\left|b\right|\end{matrix}\right.\)
\(\Rightarrow cos\left(\overrightarrow{a},\overrightarrow{b}\right)=\frac{\overrightarrow{a}\overrightarrow{b}}{\left|\overrightarrow{a}\right|\left|\overrightarrow{b}\right|}=\frac{\frac{b^2}{2}}{\left|a\right|.\left|b\right|}=\frac{\frac{b^2}{2}}{b^2}=\frac{1}{2}\)
\(\Rightarrow\left(\overrightarrow{a};\overrightarrow{b}\right)=60^0\)