Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

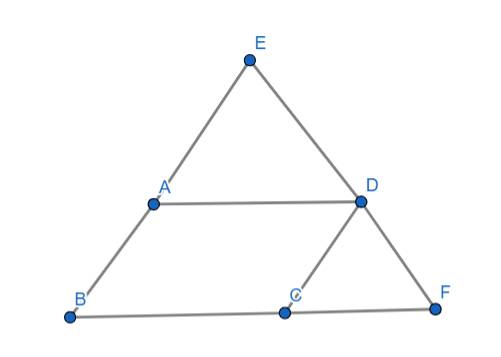
Đặt độ dài cạnh AD là a, độ dài cạnh AB là b
Ta có: ABCD là hình bình hành nên:
\(AB=CD=b\) (hai cạnh bên)
Mà: DCF là tam giác đều nên:
\(CD=CF=DF=b\) (ba cạnh tam giác đều)
Và: \(AD=BC=a\)
\(\Rightarrow BF=BC+CF=a+b\) (1)
Và: ΔADE là tam giác đều nên:
\(AD=DE=AE=a\)
\(\Rightarrow BE=AB+AE=a+b\) (2)
\(\Rightarrow EF=DE+DF=a+b\) (3)
Từ (1) và (2) và (3)
\(\Rightarrow BE=BF=EF=a+b\)
Vậy ΔBEF là tam giác đều (đpcm)

M N P Q F E
ta có: ^ENP=^NPE=^PEN=60 (vì tg PEN đều)
Do tg ABCD là hbh nên : MNQ=NPQ( 2 góc đ đ). mà FMN=NPE=60 nên MNQ+FMN=NPQ+NPE=> FMQ=QPE
xét tg MFQ và tg PQE có: MF= PQ( cùng =MN) ; MQ= PE (cùng = NP) và ^FMQ=^QPE( cmt)
=> tg MFQ= tg PQE (c.g.c) => QF=QE (1)
Ta ó : ^FNE+ENP=180(2 góc kề nhau) => => ^FNE=180-60=120 (vì ^ENP=60) (*)
Mặt khác: ^QPE+^PEN=180 (vì ME//PQ)=> ^QPE=180-6=120 (vì ^PEN=60) (**)
từu (*), (**) => ^FNE=^QPE=120
xét tg FNE và tg QPE có: FN=PQ(cùng =MN) ; ^FNE=^QPE(cmt) ; NE=PE (vì tg PEN đều)
=> tg FNE=tg QPE (c.g.c) => FE=QE (2)
Từ (1),(2) => QF=QE=FE => tg EFQ đếu
sửa lại từ chỗ " Ta có " thứ 2 nha
Dặt ^MNP=a => ^ FNE= 360- ^FNM- ^ENP- ^MNP=> ^FNE=360-60-60-a =240-a (*)
Mặt khác : MN//PQ( tg ABCD là hbh)=> MNP+NPQ=180=> NPQ=180-a=> NPQ+NPE=180-a+ 60( vì NPE=60)
=> QPE=240-a (**)
Từ (*),(**)=> ^FNE=^QPE=240-a
còn lại phần xét tg FEN và tg QPE là đúng r nha

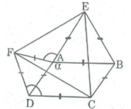
Ta có:
∠ (BAD) + ∠ ∠ (ADC) = 180 0 (hai góc trong cùng phía bù nhau)
⇒ ∠ (ADC) = 180 0 - ∠ (BAD) = 180 0 – α
∠ (CDF) = ∠ (ADC) + ∠ (ADF) = 180 0 - α 2 + 60 0 = 240 0 - α
Suy ra: ∠ (CDF) = ∠ (EAF)
Xét ∆ AEF và ∆ DCF: AF = DF ( vì ∆ ADF đều)
AE = DC (vì cùng bằng AB)
∠ (CDF) = ∠ (EAF) (chứng minh trên)
Do đó: ∆ AEF = ∆ DCF (c.g.c) ⇒ EF = CF (1)
∠ (CBE) = ∠ (ABC) + 60 0 = 180 0 - α + 60 0 = 240 0 - α
Xét ΔBCE và ΔDFC: BE = CD ( vì cùng bằng AB)
∠ (CBE) = ∠ (CDF) = 240 0 - α
BC = DF (vì cùng bằng AD)
Do đó ∆ BCE = ∆ DFC (c.g.c) ⇒ CE = CF (2)
Từ (1) và (2) suy ra: EF = CF = CE
Vậy ∆ ECF đều.