Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Ta có: \(\frac{AE}{FE}=\frac{DE}{BE}\)(theo cau a)).
\(\Rightarrow\frac{AE}{FE+AE}=\frac{DE}{BE+DE}\)(tính chất của tỉ lệ thức).
\(\Rightarrow\frac{AE}{AF}=\frac{DE}{BD}\)(4).
Lại có: \(\frac{KE}{AE}=\frac{DE}{BE}\)(theo câu a)).
\(\Rightarrow\frac{AE}{KE}=\frac{BE}{DE}\)(tính chất của tỉ lệ thức).
\(\Rightarrow\frac{AE}{KE+AE}=\frac{BE}{DE+BE}\)(tính chất của tỉ lệ thức).
\(\Rightarrow\frac{AE}{AK}=\frac{BE}{BD}\)(5).
Từ (4) và (5).
\(\Rightarrow\frac{AE}{AF}+\frac{AE}{AK}=\frac{DE}{BD}+\frac{BE}{BD}\).
\(\Rightarrow AE\left(\frac{1}{AF}+\frac{1}{AK}\right)=\frac{DE+BE}{BD}\).
\(\Rightarrow AE\left(\frac{1}{AF}+\frac{1}{AK}\right)=\frac{BD}{BD}\).
\(\Rightarrow AE\left(\frac{1}{AF}+\frac{1}{AK}\right)=1\).
\(\Rightarrow\frac{1}{AF}+\frac{1}{AK}=\frac{1}{AE}\)(điều phải chứng minh).

- Bài 1
a) Xét tam giác BCD có BM=MD(gt), BN=NC(gt) => MN là đg` TB => MN// DC => MN// DE(1)
và MN=1/2DC => MN= DE(2)
từ (1)và (2) => MNED là hbh
b) MNED là hbh(câu a) => MD//NE => ADM= DEN(đồng vị)
Xét tam giác ABD vg tại A có BM=DM=> AM là trung tuyến => AM=1/2BD= MD
=> tam giác ADM cân tại M => MDA = DAM
=> DEN= MAD (3)
MN//DE=> MN//AE => AMNE là hình thang (4)
từ (3)và (4) => AMNE là hình thang cân
c) để MNED là hình thoi \Leftrightarrow MNED là hbh có MD=DE \Leftrightarrow 1/2BD=1/2CD \Leftrightarrow BD = CD \Leftrightarrow tam giác BCD cân tại D \Leftrightarrow DBC=góc C \Leftrightarrow góc C=1/2góc B\Leftrightarrow góc C=2góc B
Vậy để MNED là hình thoi thì tam giác ABC có góc C=2góc B17 Tháng mười hai 2013#2 
nhuquynhdatGuest
bài 2
a) AB//CD => AB//CE(1)
Xét tam giác ADE có AH là đg` cao
lại có E đối xứng với D qua H => H là trung điểm của DE => AH là trung tuyến
=> tam giác ADE cân tại A
=> ADE=AED(goác đáy tam giác cân)
mặt khác ABCD là hình thang cân => ADC=góc C
=> góc C= AED
mà 2 góc này ở vị trí đồng vị của AE và BC => AE//BC(2)
từ (1)và (2) => ABCE là hbh
b) xét tam giác AHE và tam giác FHD có góc AHE=góc DHF(đối đỉnh)
DH=HE(gt)
AE//DF(gt)=> AEH=FDH(SLT)
=>tam giác AHE=tam giác FHD(gcg) => AH=HF => H là TĐ của AF
c) Ta có AH=HF(câu b)DH=HE(gt) => ADFE là hbh
mà AH vg góc với ED=> AF vg góc với ED => ADEF là hình thoi
lại có tam giác ADE cân tại A (câu a)=> AD=AE => ADEF là hình vg

Hình vẽ đây :
YAX34P43.jpg (578×558)
Bài làm để Cô Quản Lý giúp đỡ nhá bn :)
Hc tốt
A B C D E F H G I
a) Gọi I là trung điểm AF
=> AI = IF = FD = 1/3 AD = 1/3 BC = BE
Mà AI//BE ( vì AD //BC)
=> ABEI là hình bình hành.
=> EI //AB (1)
Xét tam giác AFH có: IE//AG ( theo (1) ) và I là trung điểm AF
=> E là trung điểm FG => EG = EF
Dễ dàng chứng minh được \(\Delta FHD=\Delta EGB\)=> HF = GE
=> GE = HF = EF
b ) DF = 1/3 DA => AF= 2/3 DA
BE = 1/3 BC => EC = 2/3 BC
Vì ABCD là hình bình hành => DA = BC => AF = EC
Mà AF// EC ( vì AD //BC )
=> AF//=EC
=> AECF là hình bình hành.

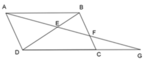
+) Vì ABCD là hình bình hành nên AD // BC => AD // BF (tính chất hbh)
Xét ΔBEF và ΔDEA có:
B E F ^ = D E A ^ (hai góc đối đỉnh)
F B E ^ = A D E ^ (cặp góc so le trong bằng nhau)
=> ΔBEF ~ ΔDEA (g - g) nên A sai
+) Vì ABCD là hình bình hành nên AB // DC => AB // DF
Xét ΔDGE và ΔBAE ta có:
D E G ^ = B E A ^ (2 góc đối đỉnh)
A B E ^ = G D E ^ (cặp góc so le trong bằng nhau)
=> ΔDGE ~ ΔBAE (g - g) nên B sai
+) Vì ΔBEF ~ ΔDEA nên E F E A = B E D E (1)
Vì ΔDGE ~ ΔBAE nên A E G E = B E D E (2)
Từ (1) và (2) ta có: E F E A = A E G E ⇔ A E 2 = GE.EF nên C đúng
Đáp án: C
Có ABCD là hình bình hành nên: AD // BC, AB // DC
A D E ^ = F B E ^ (cặp góc so le trong)
A B E ^ = E D G ^ (cặp góc so le trong)
Xét tam giác BFE và tam giác DAE có:
A D E ^ = F B E ^ (cmt)
A E D ^ = F E B ^ (đối đỉnh)
=> ΔBFE ~ ΔDAE (g - g) nên A đúng, C sai.
Xét tam giác DGE và tam giác BAE có:
A B E ^ = E D G ^ (cmt)
A E B ^ = G E D ^ (đối đỉnh)
=> ΔDGE ~ ΔBAE (g - g) hay ΔDEG ~ ΔBEA nên B, D đúng
Đáp án: C
áp dụng Ta-Lét là ra