Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E F I J
a)
Vì tứ giác ABCD là hình chữ nhật (gt)
\(\Leftrightarrow\hept{\begin{cases}\widehat{DAB}=90^o\\AB\backslash\backslash CD\\AB=CD\end{cases}}\)(tính chất hình chữ nhật)
mà AE=EB=\(\frac{AB}{2}\)(gt)
CF=FD=\(\frac{CD}{2}\)(gt)
AD=\(\frac{AB}{2}\)(gt)
\(\Rightarrow AE=EB=BC=CF=FD=AD\)(1)
Ta có:
AB//CD (cmt)
mà \(E\in AB\left(gt\right)\)
\(F\in CD\left(gt\right)\)
\(\Rightarrow\)BE//DF và AE//DF (2)
Từ (1) và (2) \(\Rightarrow\)tứ giác DEBF là hình bình hành (dấu hiệu nhận biết hình bình hành)
b) Tứ giác IEJF là hình vuông. Thật vậy:
Vì tứ giác DEBF là hình bình hành (cmt)
\(\Rightarrow\)DE//BF (tính chất hình bình hành)
mà \(I\in DE\left(gt\right)\)
\(J\in BF\left(gt\right)\)
=> IE//JF (3)
cmtt\(\Rightarrow\)JE//IF (4)
Từ (1) và (2)\(\Rightarrow\)tứ giác AEFD là hình bình hành(dấu hiệu nhận biết hình bình hành)
mà AE=AD (cmt)
\(\Rightarrow\)tứ giác AEFD là hình thoi(dấu hiệu nhận biết thoi)
\(\Leftrightarrow\hept{\begin{cases}AB\backslash\CD\\AB=CD\end{cases}}\)mà \(\widehat{DAB}=90^o\left(cmt\right)\)
\(\Rightarrow\)tứ giác AEFD là hình vuông(dấu hiệu nhận biết hình vuông)
\(\Rightarrow\hept{\begin{cases}IE=IF\\\widehat{EIF}=90^o\end{cases}}\)(tính chất hình vuông) (5)
Từ (3), (4), (5)
\(\Rightarrow\)tứ giác IEJF là hình vuông (dấu hiệu nhận biết hình vuông)

a: Xét tứ giác DEBF có
BE//DF
BE=DF
Do đó: DEBF là hình bình hành
b: ta có: DEBF là hình bình hành
nên Hai đường chéo DB và EF cắt nhau tại trung điểm của mỗi đường(1)
Ta có:ABCD là hình bình hành
nên hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra BD,EF,AC đồng quy

Mình sửa lại đề 1 chút: AC=a; BD=b
d) \(MN=\frac{AC}{3}=\frac{a}{2}\)
d(E,MN)=\(\frac{BD}{2}=\frac{b}{2}\)
\(\Rightarrow S_{MENF}=S_{MEN}+S_{MEF}=\frac{1}{2}\cdot2\cdot MN\cdot d\left(E,MN\right)\)
\(=2S_{MEN}=\frac{a}{3}\cdot\frac{b}{2}=\frac{ab}{6}\)

a) Tứ giác DEBF là hình bình hành vì có 2 cạnh đối // và bằng nhau
b) Vì DEBF là hình bình hành nên EF và BD giao nhau tại trung điểm của BD
Vì ABCD cũng là hình bình hành nên AC và BD cũng giao nhau tại trung điểm của BD
=> AC,BD, EF đồng quy
c) Gọi O là giao điểm của AC và BD
Tam giác ABD có M là trọng tâm=> ME=\(\frac{1}{3}\)DE
Chứng minh tương tự trong tam giác BCD => NF=\(\frac{1}{3}\)BF
mà DE=BF( do DEBF là hình bình hành) => ME=NF và có ME//NF (do DE//BF)=> EMFN là hình bình hành
Mình chỉ trình bày ngắn gọn để bạn hiểu hướng giải bài thôi!!! Khi trình bày vào vở bạn phải trình bày chi tiết ra chứ đừng có trình bày như mình nha!!

b tham khảo nha
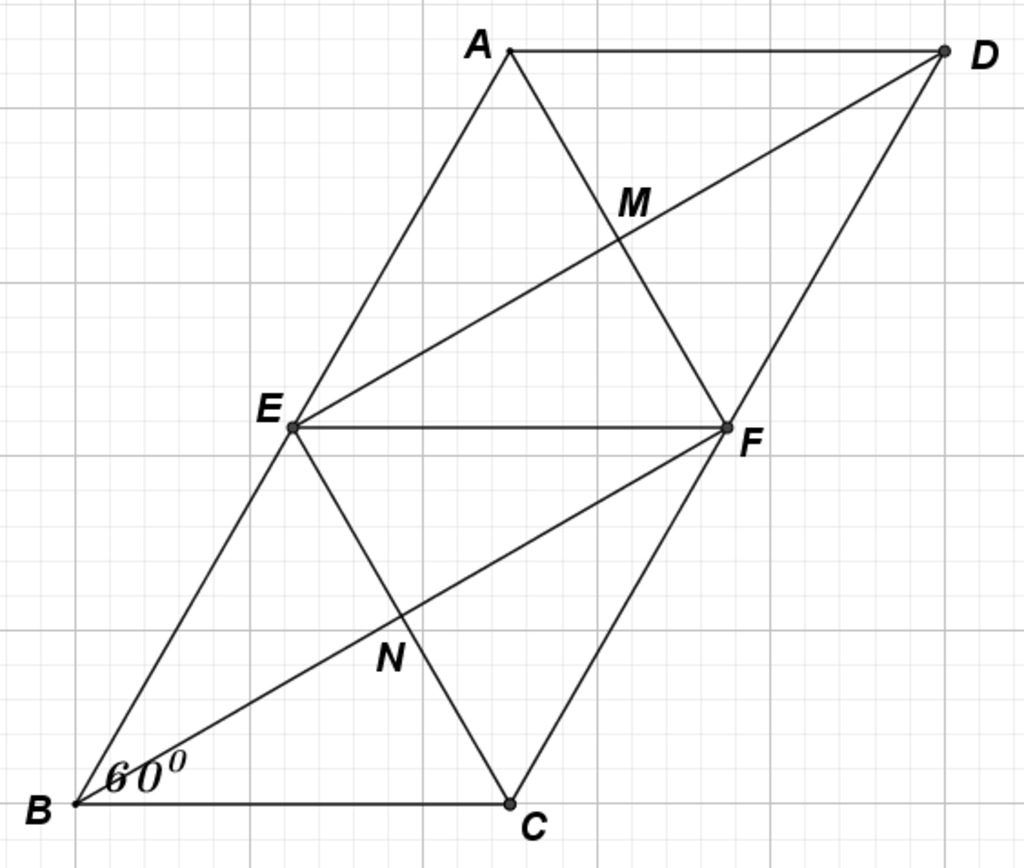
a) Do ABCD là hình bình hành nên AB= CD và AB//CD
Và E và F là trung điểm của AB và CD => AE=BE=CF=DF và BE//DF
Xét tứ giác DEBF có : BE//DF và BE=DF=> DEBF là hình bình hành
b)
Xét AEDF có AE//DF và AE=DF=> AEDF là hình bình hành
Lại có: CD= 2BC= 2 AD nên AD= AE (=1/2 CD)
=> hình bình hành AEDF là hình thoi
c)ta cm được AECF là hình bình hành và M, N là trung điểm của AF và CE
=> MF= EN và MF//EN=> EMFN là hình bình hành
Lại có AEDF là hình thoi nên AN⊥DE tại M
=> góc EMF vuông=> hình bình hành EMFN là hình chữ nhật
d) Chứng minh được
SAFB=12SABCDSBEC=14SABCDˆB=600⇒ΔBECdeucanh=AB2=2(cm)⇒SBEC=√3(cm2)⇒SAFB

A D C B E O F M N
a) Trong tứ giác DEBF có:
Hai đường chéo BD và EF cắt nhau tại trung điểm O
Các cạnh đối BE và DF bằng nhau
\(\Rightarrow\) Tứ giác DEBF là hình bình hành.
b) Gọi O là giao điểm hai đường chéo của hình bình hành ABCD, ta có O là trung điểm của BD.
Theo câu a), DEBF là hình bình hành nên trung điểm O của BD cũng là trung điểm của EF.
Vậy AC, BD, EF cùng cắt nhau tại điểm O.
c) \(\Delta ABD\) có các đường trung tuyến AO, DE cắt nhau ở M nên OM = \(\dfrac{1}{3}\) OA.
\(\Delta CBD\) có các đường trung tuyến CO, BF cắt nhau ở N nên ON = \(\dfrac{1}{3}\) OC.
Tứ giác EMFN có các đường chéo cắt nhau tại trung điểm của mỗi đường OM = ON, OE = OF nên là hình bình hành.

Xét tứ giác DEBF, ta có:
AB // CD (gt) hay DF // EB
EB = 1/2 AB (gt)
DF = 1/2 CD (gt)
Suy ra: EB = DF
Tứ giác DEBF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).