Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo giả thiết, do AH và CK cùng vuông góc BD
=> AH song song CK (1)
Do AH vuông góc BD và CK vuông góc BD nên các tam giác ABH và tam giác CDK là các tam giác vuông.
Xét hai tam giác vuông ABH và CDK có:
AB=CD (hai cạnh đối hình bình hành)
∠ABH=∠CDK (hai góc so le trong)
\(\Rightarrow\Delta_{\bot}ABH=\Delta_{\bot}CDK\) (cạnh huyền - góc nhọn)
=>AH=CK (2)
Từ (1) và (2) =>AHCK là hbh

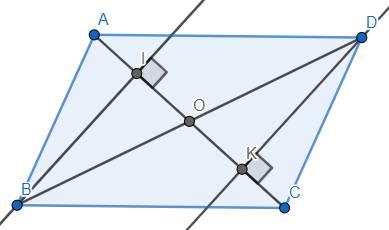
b) Vì BI vuông góc với AC tại I, nên I thuộc AC.
Vì DK vuông góc với AC tại K, nên K thuộc AC.
Vì O là giao điểm của AC và BD nên O thuộc AC.
Suy ra I, O, K là các điểm thuộc AC; từ đó ba điểm I, O, K thẳng hàng

Trả lời:
a) Xét tam giác AHI và AKI có :
AI là cạnh chung
góc HAI =góc KAI
góc H = góc K (=90)
suy ra tam giác AHI = tam giác AKI (cạnh huyền - góc nhọn )
suy ra góc AIH =AIK (hai góc tg ứng)
suy ra góc HIB = KIC (cùng kề vs hai góc bằng nhau )
xét tam giác HIB và KIC có
HIB = KIC (chứng minh trên )
BHI=CKI (=90)
BI=IC
suy ra tam giác HIB=KIC(cạnh huyền góc nhọn )
suy ra BH=CK ( hai cạnh tương ứng ) (điều phải chứng minh )
b) Xét tam giác AHI và AKI có :
AI là cạnh chung
góc HAI =góc KAI
góc H = góc K (=90)
suy ra tam giác AHI = tam giác AKI (cạnh huyền - góc nhọn )
suy ra góc AIH =AIK (hai góc tg ứng)
suy ra góc HIB = KIC (cùng kề vs hai góc bằng nhau )
xét tam giác HIB và KIC có
HIB = KIC (chứng minh trên )
BHI=CKI (=90)
BI=IC
suy ra tam giác HIB=KIC(cạnh huyền góc nhọn )
suy ra BH=CK ( hai cạnh tương ứng ) (đpcm)
~Học tốt!~

BTS là cục cứt chó j , nó đéo xứng làm cục cứt của the coconut tao
con kia là đồ giả mạo
Mà ông Duy có j hay đâu mà bọn m giả lắm thế
Từ giả thiết ta có AH song song CK (1) (cùng vuông góc BD)
Xét hai tam giác vuông ABH và CDK có:
AB=DC (ABCD là hình bình hành)
∠ABH=∠CDK (so le trong)
\(\Rightarrow\Delta_{\bot}ABH=\Delta_{\bot}CDK\left(\ch-gn\right)\)
=>AH=CK (2)
Từ (1) và (2) =>AHCK là hbh (tứ giác có cặp cạnh đối song song và bằng nhau)
ta có
\(A H \bot B D\), \(C K \bot B D\)
⇒ \(A H \parallel C K\) (hai đường cùng vuông góc với một đường thẳng thì song song với nhau)
Trong hình bình hành \(A B C D\): \(A C \parallel B D\)
Mà \(A H \bot B D\), \(C K \bot B D\) ⇒ \(A H , C K \bot A C\)
⇒ \(H C \parallel A K\)
Vậy
tứ giác \(A H C K\) có hai cặp cạnh đối song song
Do đó \(A H C K\) là hình bình hành