Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi I là tâm của hình vuông thì I chính là hình chiếu của C lên BD
Ta có: I ( -1+4t;1-t;-1+t )nên C I → = 4 t - 2 ; 2 - t ; t + 1
Vì C I ⊥ B D nên
C I ⇀ . u B D → = 0 ⇔ 4 4 t - 2 - 2 - t + t + 1 = 0 ⇔ t = 1 2
Do đó: I 1 ; 1 2 ; - 1 2 , C I - 3 2 2
I là trung điểm AC ⇒ A ( 1;2;3 )
Tọa độ điểm B - 1 + 4 t ; 1 - t ; - 1 + t với t > 1 4
Ta có IB = IC nên
- 2 + 4 t 2 + 1 2 - t 2 + 1 2 + t 2 = 9 2 ⇔ t 2 - t = 0 ⇔ t = 0 t = 1
Tọa độ điểm B ( 3;0;0 ). Suy ra d ( -1;1;-1 )
Đáp án D

Giả sử C(c,3-c). Gọi I là giao điểm của AC và MN, suy ra \(\overrightarrow{AI}=\dfrac{2}{3}\overrightarrow{AC}=\left(\dfrac{2(c+2)}{3};\dfrac{2(3-c)}{3}\right)\)
Do đó \(I\left(\dfrac{2c-2}{3};\dfrac{6-2c}{3}\right)\in MN:7x-6y-5=0\Rightarrow c=\dfrac{5}{2}\). Vậy \(C\left(\dfrac{5}{2};\dfrac{1}{2}\right)\)
Trung điểm của AC là \(P\left(\dfrac{1}{4};\dfrac{1}{4}\right),\overrightarrow{AC}\left(\dfrac{7}{2};\dfrac{1}{2}\right)\Rightarrow B\left(\dfrac{1}{4}+t;\dfrac{1}{4}-7t\right), D\left(\dfrac{1}{4}-t;\dfrac{1}{4}+7t\right)\).
Vì \(BP=CP=\dfrac{AC}{2}=\dfrac{5\sqrt{2}}{2}\)nên \(t=\pm\dfrac{1}{2}\)
Vậy \(B\left(\dfrac{3}{4};-\dfrac{13}{4}\right),D\left(-\dfrac{1}{4};\dfrac{15}{4}\right)\)hoặc \(B\left(-\dfrac{1}{4};\dfrac{15}{4}\right),D\left(\dfrac{3}{4};-\dfrac{13}{4}\right)\).


Đáp án D
Ta có D N = B M = 1 3 B D ⇒ D N = 2 3 D O B M = 2 3 B O ⇒ M , N lần lượt là trọng tâm tam giác ABC, ACD
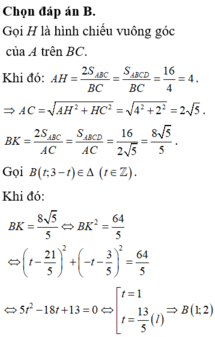


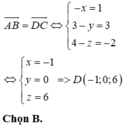

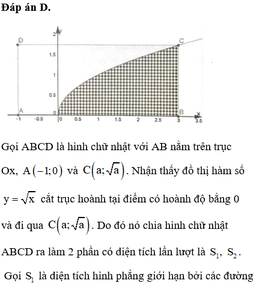

Dễ thấy pt (AB): y=0 : trục hoành
Gọi H là chân đường vuông góc kẻ từ I đến AB, đặt IH=a
=> I(a;a) ( do (AB) là trục hoành và I thuộc đường thẳng x=y)
*Sử dụng công thức diện tích hình bình hành=> tính được IH => tọa độI ( hai trường hợp)
Vì I là trung điểm AC, BD => tọa độ C,D