Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

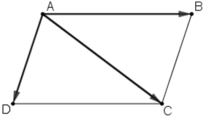
Ta chứng minh hai mệnh đề:
- Khi =
thì ABCD là hình bình hành.
Thật vậy, theo định nghĩa của vec tơ bằng nhau thì:
=
⇔
=
và và
cùng hướng.
và
cùng hướng =>
và
cùng phương, suy ra giá của chúng song song với nhau, hay AB // DC (1)
Ta lại có =
=> AB = DC (2)
Từ (1) và (2), theo dấu hiệu nhận biết hình bình hành, tứ giác ABCD có một cặp cạnh song song và bằng nhau nên nó là hình bình hành.
- Khi ABCD là hình bình hành thì =
Khi ABCD là hình bình hành thì AB // CD. Dễ thấy, từ đây ta suy ra hai vec tơ và
cùng hướng (3)
Mặt khác AB = CD => =
(4)
Từ (3) và (4) suy ra =
.

ta có \(\hept{\begin{cases}\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}\Rightarrow AC^2=AB^2+BC^2+2\overrightarrow{AB}.\overrightarrow{BC}\\\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{AD}\Rightarrow BD^2=BA^2+AD^2+2\overrightarrow{BA}.\overrightarrow{AD}\end{cases}}\)
mà \(\overrightarrow{AB}.\overrightarrow{BC}+\overrightarrow{BA}.\overrightarrow{AD}=\overrightarrow{AB}.\overrightarrow{BC}+\overrightarrow{AB}.\overrightarrow{AD}=0\)
Do đó \(AC^2+BD^2=2AB^2+2BC^2\Leftrightarrow m^2+n^2=2\left(a^2+b^2\right)\)

\(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AC}\)
ABCD là hình bình hành nên
\(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\) (quy tắc hình bình hành của tổng)
\(\Rightarrow\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=\overrightarrow{AC}+\overrightarrow{AC}=2\overrightarrow{AC}\)

Áp dụng định lí về đường trung tuyến:
OA2 = -
(1)
Thay OA = , AB = a, AD = BC = b và BD = m vào (1) ta có:
\(\left(\dfrac{n}{2}\right)^2=\dfrac{b^2+a^2}{2}-\dfrac{m^2}{4}\)
\(\Leftrightarrow\dfrac{n^2}{4}+\dfrac{m^2}{4}=\dfrac{a^2+b^2}{2}\)
\(\Leftrightarrow m^2+n^2=2\left(a^2+b^2\right)\)
A B C D a b n m

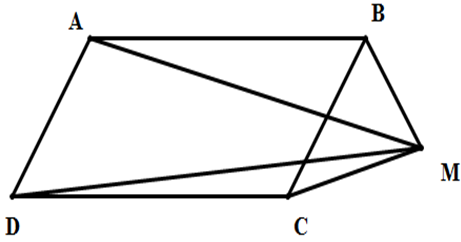
Do là giao điểm của hai đường chéo hình bình hành nên:
\(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}\)\(=\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{MO}+\overrightarrow{OC}+\overrightarrow{MO}+\overrightarrow{OD}\)
\(=4\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}\)
\(=4\overrightarrow{MO}\) (ĐPCM).

A B C D O
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\left(\overrightarrow{OA}+\overrightarrow{OC}\right)+\left(\overrightarrow{OB}+\overrightarrow{OC}\right)\)
\(=\overrightarrow{0}+\overrightarrow{0}\)(Theo tính chất hình bình hành).
\(=\overrightarrow{0}\) .

Áp dụng định lí về đường trung tuyến:
OA2 = –
Thay OA = , AB = a
AD = BC = b và BD = m => dpcm
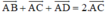
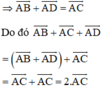
ABCD là hình bình hành nên
=> +
+ 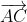 +
+ 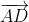 =
= 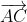 +
+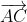 =2
=2