Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

*Khi quay hình bình hành ABCD một vòng quanh cạnh AB thì cạnh AD và BC vạch nên hai hình nón bằng nhau có đường sinh AD = BC = x, cạnh CD vạch nên hình trụ có bán kính đáy bằng bán kính hình nón
Trong tam giác AHD,ta có:
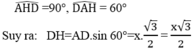
Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh của hai hình nón và diện tích xung quanh của hình trụ
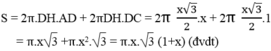
*Khi quay hình bình hành ABCD một vòng quanh AD thì cạnh AB và DC vạch nên hai hình nón bằng nhau có đường sinh AB = DC = 1, cạnh BC vạch nên hình trụ có bán kính đáy bằng bán kính đáy của hình nón
Ta có:
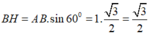
Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh của hai hình nón và diện tích xung quanh của hình trụ
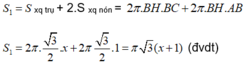

Ta có AB//CD
\(\Rightarrow\widehat{DAB}+\widehat{ADC}=180\\ \Rightarrow\widehat{ADC}+135=180\\ \Rightarrow\widehat{ADC}=45\)
Ta có \(\sin D=\sin45=\dfrac{AH}{AD}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\dfrac{AH}{15}=\dfrac{\sqrt{2}}{2}\left(cm\right)\\ \Rightarrow AH=\dfrac{15\sqrt{2}}{2}\left(cm\right)\\ \Rightarrow S_{ABCD}=AB\cdot AH=18\cdot\dfrac{15\sqrt{2}}{2}=135\left(cm^2\right)\)

hình bạn tự vẽ nhé
a) vì A=45o và AB=BD
=>ABD là tam giác vuông cân
=>AD2=AB2+BD2
=>AD2=182+182
=>AD2=648
=>AD=\(18\sqrt{2}\)
b) ABD là tam giác vuông cân ; AB //CD
=>ABD=BDC=90o
=>BD là đường cao của ABCD
Vậy diện tích vủa hình bình hành
AB.BD=18.18=324

bạn kiếm câu này ở đâu z mình đang luyện thi toán casio mà câu này khó quá bạn có biết chỉ mình

GIẢI:
a) Chứng minh tam giác CKH đồng dạng tam giác BCA
AKC^ + ABC^ = 2v => AKCH nội tiếp
=> CHK^ = CAB^ (1) ( cùng chắn cung CK)
CKH^ = CAH^ (2) ( cùng chắn cung CH)
CAH^ = ABC^ (3) ( so le trong)
(2) và (3) => CKH^ = ACB^ (4)
(1) và (4) => ΔCKH ~ ΔBCA (g.g)
b) Chứng minh HK=AC.sinBAD
ΔCKH ~ ΔBCA =>HK/AC = CH/AB = CH/CD = sin(CDH^) = sin(BAD^) ( đồng vị)
=> HK = AC.sin(BAD^)
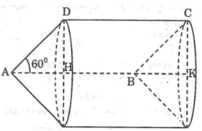
c) Tính diện tích tứ giác AKCH nếu góc BAD = 60 độ, AB=4cm, AD=5cm
AB = CD = 4
CDH^ = BAD^ = 60*
=> CH = 4√3/2 = 2√3 ( đường cao tam giác đều cạnh = 4)
DH = CD/2 = 4/2 = 2
=> AH = AD + DH = 5 + 2 = 7
AD = BC = 5
CBK^ = BAD^ = 60*
=> CK = 5.√3/2
BK = BC/2 = 5/2
=> AK = AB + BK = 4 + 5/2 = 13/2
S(AKCH) = S(ACK) + S(ACH) = AK.CK/2 + AH.CH/2
= (13/2).( 5.√3/2)/2 + 7.(2√3)/2 = 732√3/8
chúc bạn học tốt

Do ABCD là hình bình hành \(\Rightarrow\widehat{B}=180^0-\widehat{BAD}=70^0\)
Kẻ đường cao AH ứng với BC
Trong tam giác vuông ABH:
\(sinB=\dfrac{AH}{AB}\Rightarrow AH=AB.sinB\)
\(\Rightarrow S_{ABCD}=AH.AD=AB.AD.sinB=12.15.sin70^0\approx169,1\left(cm^2\right)\)