
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔBKC có
H là trung điểm của BC
BI//KC
Do đó: I là trung điểm của BK
b: Xét ΔKBH có
I là trung điểm của BK
F là trung điểm của HK
Do đó: IF là đường trung bình
=>IF//BH
hay IF\(\perp\)AH

ttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttt
ABCHKIEF
a)
Xét \(\Delta\)ABC và \(\Delta\)HBA có:
^BAC = ^BHA ( = 90 độ )
^ABC = ^HBA ( ^B chung )
=> \(\Delta\)ABC ~ \(\Delta\)HBA
b) AB = 3cm ; AC = 4cm
Theo định lí pitago ta tính được BC = 5 cm
Từ (a) => \(\frac{AB}{BH}=\frac{BC}{AB}\Rightarrow BH=\frac{AB^2}{BC}=1,8\)m
c) Xét \(\Delta\)AHC và \(\Delta\)AKH có: ^AKH = ^AHC = 90 độ
và ^HAC = ^HAK ( ^A chung )
=> \(\Delta\)AHC ~ \(\Delta\)AKH
=> \(\frac{AH}{AK}=\frac{AC}{AH}\Rightarrow AH^2=AC.AK\)
d) Bạn kiểm tra lại đề nhé!

3 cm 4cm 5 cm 1cm 1cm O H I K O'
XÉT 2 TAM GIÁC HIM VÀ HOM CÓ
+,HI=HO(=3CM)
+,∠MHI=∠MHO
+,CHUNG CẠNH HM
SUY RA:▲HIM=▲HOM(C.G.C)
⇒MI=MO(2 CẠNH TƯƠNG ỨNG)
⇒∠HIM=∠HOM(2 GÓC TƯƠNG ỨNG)
⇒∠MOK=∠MIO'(VÌ CÙNG BÙ VỚI ∠HIM VÀ ∠HOM)
XÉT 2 TAM GIÁC KOM VÀ O'IM CÓ
OI=OM
IO'=OK=1CM
∠MOK=∠MIO'
⇒▲KOM=▲O'MI(C.G.C)
⇒IM=IK(2 CẠNH TƯƠNG ỨNG)
TA CÓ:IM+IK=5CM
⇒IM✖2=IK✖2=5CM
⇒IM=IK=2,5
VẬY IM=IK=2.5 CM

Theo câu a) ta có: \(AH^2=AI.AB\left(1\right)\)
Xét tam giác AHK và tam giác ACH có:
góc A chung; góc AKH = góc AHC = 900
=> tam giác AHK đồng dạng với tam giác ACH (g-g)
=>\(\dfrac{AK}{AH}=\dfrac{AH}{AC}\Rightarrow AK.AC=AH^2\left(2\right)\)
Từ (1)(2) => \(AI.AB=AK.AC\Rightarrow\dfrac{AI}{AC}=\dfrac{AK}{AB}\)
Xét tam giác AIK và tam giác ABC có:
góc A chung; \(\dfrac{AI}{AC}=\dfrac{AK}{AB}\)
=> Tam giác AIK đồng dạng với tam giác ACB (c-g-c)
a) Xét tam giác AIH và tam giác AHB có:
góc BAH chung; góc AIH = góc AHB (= 900)
=> tam giác AIH = tam giác AHB (g-g)
\(\Rightarrow\dfrac{AH}{AI}=\dfrac{AB}{AH}\Rightarrow AH^2=AI.AB\)

hình bạn tự vẽ nhé
a) Ta có : \(\frac{HI}{AI}=\frac{S_{HIC}}{S_{AIC}}=\frac{S_{HIB}}{S_{AIB}}=\frac{S_{HIC}+S_{HIB}}{S_{AIC}+S_{AIB}}=\frac{S_{BHC}}{S_{ABC}}\)
Tương tự : \(\frac{HK}{BK}=\frac{S_{AHC}}{S_{ABC}}\); \(\frac{HS}{CS}=\frac{S_{AHB}}{S_{ABC}}\)
\(\Rightarrow\frac{HI}{AI}+\frac{HK}{BK}+\frac{HS}{CS}=\frac{S_{AHC}+S_{BHC}+S_{AHB}}{S_{ABC}}=1\)
b) tương tự câu a : \(\frac{HA_1}{AI}=\frac{2HI}{AI}=\frac{2S_{BHC}}{S_{ABC}}\).....

a: Xét ΔAHB vuông tại H và ΔCHA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\)
Do đó: ΔAHB\(\sim\)ΔCHA
b: Xét ΔAHB vuông tại H có HI là đường cao
nên \(AI\cdot AB=AH^2\left(1\right)\)
Xet ΔAHC vuông tại H có HK là đường cao
nên \(AK\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AI\cdot AB=AK\cdot AC\)
hay AB/AK=AC/AI
Xét ΔABC vuông tại A và ΔAKI vuông tại A có
AB/AK=AC/AI
Do đó: ΔABC\(\sim\)ΔAKI
d: \(IB\cdot BC\cdot CK=\dfrac{BH^2}{AB}\cdot\dfrac{CH^2}{AC}\cdot BC\)
\(=\dfrac{\left(BH\cdot CH\right)^2}{AB\cdot AC}\cdot BC=\dfrac{AH^4}{AH\cdot BC}\cdot BC=AH^3\)
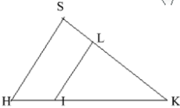
Ta có:
+ SL/LK = HI/IK → SH//LI
+ SL/SK = HI/HK → SH//LI
Chọn đáp án B.