
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Để phân thức được xác định thì
x3-8\(\ne\)0
<=> (x-2)(x2+2x+4)\(\ne\) 0
\(< =>\left[\begin{matrix}x-2\ne0\\x^2+2x+4\ne0\end{matrix}\right.\Leftrightarrow\left[\begin{matrix}x\ne2\\x^2+2x+4>0\end{matrix}\right.\)
Vậy ĐKXĐ x\(\ne\)2
b)\(\frac{3x^2+6x+12}{x^3-8}=\frac{3\left(x^2+2x+4\right)}{\left(x-2\right)\left(x^2+2x+4\right)}=\frac{3}{x-2}\)
c) Với x = \(\frac{4001}{2000}\) thì \(\frac{3}{\frac{4001}{2000}-2}\) =6000
CHÚC BẠN HỌC TỐT!!
a) Điều kiện các định khi \(x^3-8\ne0\)
\(\Rightarrow\left(x-2\right)\left(x^2+2x+4\right)\ne0\)
\(\Rightarrow\left[{}\begin{matrix}x-2\ne0\\x^2+2x+4\ne0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x\ne2\\\left(x+1\right)^2+3>0\left(loai\right)\end{matrix}\right.\)
\(\Rightarrow\) điều kiện xác định khi \(x\ne2\)
b) \(\dfrac{3x^2+6x+12}{x^3-8}\)
\(=\dfrac{3\left(x^2+2x+4\right)}{\left(x-2\right)\left(x^2+2x+4\right)}\)
\(=\dfrac{3}{x-2}\)
c) Thay \(x=\dfrac{4001}{2000}\) vào biểu thức trên ta được:
\(\dfrac{3}{\dfrac{4001}{2000}-2}\)
\(=\dfrac{3}{\dfrac{4001}{2000}-\dfrac{4000}{2000}}\)
\(=\dfrac{3}{\dfrac{4001-4000}{2000}}\)
\(=\dfrac{3}{\dfrac{1}{2000}}\)
\(=6000\)
Vậy giá trị của biểu trên tại \(x=\dfrac{4001}{2000}\) là \(6000\)

a) Ta có: P(x) = 3y + 6 có nghiệm khi
3y + 6 = 0
3y = -6
y = -2
Vậy đa thức P(y) có nghiệm là y = -2.
b) Q(y) = y4 + 2
Ta có: y4 có giá trị lớn hơn hoặc bằng 0 với mọi y
Nên y4 + 2 có giá trị lớn hơn 0 với mọi y
Tức là Q(y) ≠ 0 với mọi y
Vậy Q(y) không có nghiệm.

Bài 1:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{CA}{2}=\dfrac{CB}{3}=\dfrac{CA+CB}{2+3}=\dfrac{20}{5}=4\)
Do đó: CA=8cm; CB=12(cm)
b: AC/AB=m/n
nên AB/AC=n/m
=>AB/AC-1=n/m-1
=>CB/CA=(n-m)/m

a) Điều kiện xác định: \(x-2\ne0\Rightarrow x\ne2\)
\(\dfrac{2x^2-8}{x-2}=\dfrac{2\left(x^2-4\right)}{x-2}=\dfrac{2\left(x-2\right)\left(x+2\right)}{x-2}=2\left(x+2\right)\)
b) \(2\left(x+2\right)=2\)
\(\Rightarrow x+2=1\)
\(\Rightarrow x=-1\)
Vậy để phân thức trên bằng 2 thi \(x=-1\)
a) \(\dfrac{2x^2-8}{x-2}=\dfrac{2\left(x^2-4\right)}{x-2}=\dfrac{2\left(x^2-2^2\right)}{x-2}=\dfrac{2\left(x-2\right)\left(x+2\right)}{x-2}=2\left(x+2\right)\)
b)x=2 <=>2(x+2)=2
<=>2x+4=2
<=>2x=-2
<=>x=-1
vậy giá trị x=-1 để giá trị của phân thức trên bằng 2

a,\(A\) xác định \(\Leftrightarrow\left[{}\begin{matrix}x+1\ne0\\1-x^2\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ne-1\\x\ne1\end{matrix}\right.\)
Vậy...
b,\(A=\dfrac{x}{x+1}:\dfrac{1-3x^2}{1-x^2}\)
\(=\dfrac{x}{x+1}:\dfrac{-\left(3x^2-1\right)}{-\left(x^2-1\right)}\)
\(=\dfrac{x}{x+1}:\dfrac{3x^2-1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x}{x+1}.\dfrac{\left(x-1\right)\left(x+1\right)}{3x^2-1}\)
\(=\dfrac{x}{1}.\dfrac{x-1}{3x^2-1}\)
\(=\dfrac{x^2-x}{3x^2-1}\)
Câu a :
Để phân thức được xác định thì :
\(\left\{{}\begin{matrix}x+1\ne0\\1-x^2\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ne-1\\x\ne1\end{matrix}\right.\)
Câu b :
\(\dfrac{x}{x+1}:\dfrac{1-3x^2}{1-x^2}\)
\(=\dfrac{x}{x+1}:\dfrac{-\left(1-3x^2\right)}{x^2-1}\)
\(=\dfrac{x}{x+1}:\dfrac{3x^2-1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x}{x+1}\times\dfrac{\left(x-1\right)\left(x+1\right)}{3x^2-1}\)
\(=\dfrac{x\left(x-1\right)\left(x+1\right)}{\left(x+1\right)\left(3x^2-1\right)}=\dfrac{x\left(x-1\right)}{3x^2-1}\)
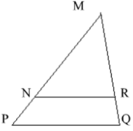
Ta có:
Cả 3 đáp án A, B, C đều sai.
Chọn đáp án D.