PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TM
5
21 tháng 11 2017
nh 98): Xét ΔABC và ΔABD có:
Nên ΔABC = ΔABD (g.c.g)
- Hình 99): Ta có:
Xét ΔABD và ΔACE có:
Nên ΔABD = ΔACE ( g.c.g)
Xét ΔADC và ΔAEB có:
DC = EB (Vì DC = DB + BC ; EB = EC + BC mà DB = EC)
Nên ΔADC = ΔAEB (g.c.g)
TH
21 tháng 11 2017
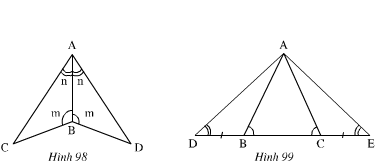
Xem hình 98)
∆ABC và ∆ABD có:
ˆA1A1^=ˆA2A2^(gt)
AB là cạnh chung.
ˆB1B1^=ˆB2B2^(gt)
Nên ∆ABC=∆ABD(g.c.g)
Xem hình 99)
Ta có:
ˆB1B1^+ˆB2B2^=1800 (Hai góc kề bù).
ˆC1C1^+ ˆC2C2^=1800 (Hai góc kề bù)
Mà ˆB2B2^=ˆC2C2^(gt)
Nên ˆB1B1^=ˆC1C1^
* ∆ABD và ∆ACE có:
ˆB1B1^=ˆC1C1^(cmt)
BD=EC(gt)
ˆDD^ = ˆEE^(gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
ˆDD^=ˆEE^(gt)
ˆC2C2^=ˆB2B2^(gt)
DC=EB
Nên ∆ADC=∆AEB(g.c.g)
19 tháng 4 2017
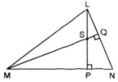
a) Từ hình vẽ ta có: LP ⊥ MN; MQ ⊥ LN
ΔMNL có S là giao điểm của hai đường cao LP và MQ nên S chính là trực tâm của tam giác (định lí ba đường cao).
=> NS cũng là đường cao trong tam giác hay NS ⊥ LM (đpcm).
b) ΔNMQ vuông tại Q có góc LNP = 50o nên góc QMN = 40o
ΔMPS vuông tại P có góc QMP = 40o nên góc MSP = 50o
Vì hai góc MSP và PSQ là hai góc kề bù nên suy ra:
góc PSQ = 180o - 50o = 130o.
19 tháng 4 2017
Hướng dẫn:
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay
SN ⊥ ML
b) ∆NMQ vuông tại Q có ˆLNPLNP^ =500 nên ˆQMNQMN^ =400
∆MPS vuông tại Q có ˆQMPQMP^ =400 nên ˆMSPMSP^ =500
Suy ra ˆPSQPSQ^ =1300(kề bù)
T
18 tháng 4 2019
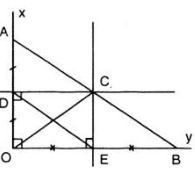
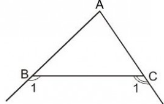
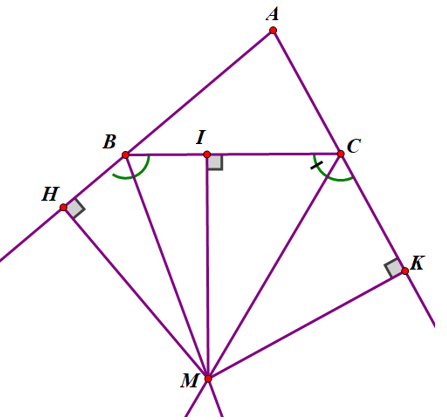
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC.
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC (như hình vẽ)
(H ∈ tia AB, I ∈ BC, K ∈ tia AC)
Theo định lí 1: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài )
MI = MK ( Vì M thuộc phân giác của góc C ngoài )
Suy ra: MH = MK (cùng bằng MI)
Dựa vào định lí 2: Điểm nằm bên trong góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
⇒ M thuộc phân giác của góc BAC (đpcm).
SK
2
GC
2
GW
21 tháng 9 2021
Đáp án :
\(-3\notinℕ\)
\(-3\in Z\)
\(-3\in Q\)
\(\frac{-2}{3}\notin Z\)
\(\frac{-2}{3}\in Q\)
\(N\subset Z\subset Q\)
21 tháng 9 2021
tả lời minh ko biết đánh kí hiệu nên là vậy nha
-3 ko thuộc N / -3 thuộc Z / -3 thuộc Q
-2/3 ko thuộc Q / -2/3 thuộc Q / N là tập hợp con của Z mà Z lại là tập hợp con của Q
chúc bn có 1 năm học mới vui vẻ
NC
12 tháng 10 2018
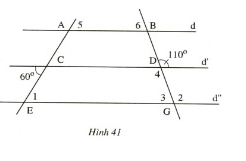
1) Tính góc ∠E1
Ta có d’//d” (gt)
⇒ ∠C = ∠E1 ( So le trong)
⇒ ∠E1 = 600 vì ∠C = 600
2) Tính ∠G3
Ta có d’//d”
⇒ ∠G2 = ∠D (Đồng vị)
⇒ ∠G1 = 1100
3) Tính ∠G3
Vì ∠G2 + ∠G3 = 1800 (kề bù)
⇒ ∠G3 = 700
4) Tính ∠D4
∠D4 = ∠D (Đối đỉnh)
⇒ ∠D4 = 1100
5) Tính ∠A5
Ta có d//d”
⇒ ∠A5 = ∠ E1 (Đồng vị)
⇒ ∠A5 = 600
6) Tính ∠B6
Ta có d//d”
⇒ ∠B6 = ∠G3 (Đồng vị)
⇒ ∠B6 = 700
HN
12 tháng 5 2017
Gọi I là giao điểm của AE và BC
Dễ thấy MA = MB = MC = ME
=> ∆AME cân
=> góc MAE = góc MEA
=> ∆ AMC cân
=> góc MAC = góc MCA
Mà ta có:
góc MEI + góc MIE = 90°
=> góc MAI + góc MIE = 90°
=> góc MAI + góc BIA = 90°
=> góc MAI + góc IAC + góc ACI = 90°
=> góc MAI + góc MAI + góc MAC + góc ACM = 90°
=> 2góc MAI + 2góc MAC = 90°
=> 2góc IAC = 90°
=> góc IAC = 45°
=> AE là phân giác của góc BAC
TH
12 tháng 5 2017
Xét tam giác BME và tam giác CME có:
EM: cạnh chung.
MB = MC (gt)
góc BME = góc CME = 90 độ
suy ra: tam giác BME = tam giác CME ( cgv-cgv)
Suy ra : EB=EC.
Nên: E thuộc tia phân giác của góc A.
Vậy: AE là TPG của góc BAC
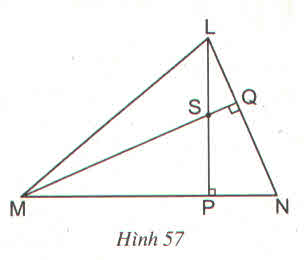
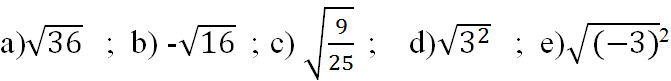
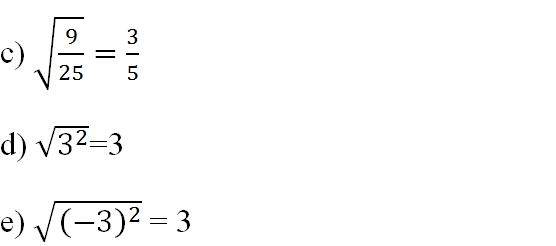
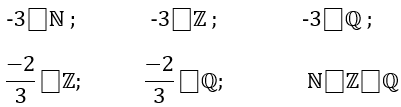
Trong ΔMNL có:
LP ⊥ MN nên LP là đường cao của ΔMNL.
MQ ⊥ NL nên MQ là đường cao của ΔMNL.
Mà LP, MQ cắt nhau tại điểm S
Nên: theo tính chất ba đường cao của một tam giác, S là trực tâm của tam giác.
⇒ đường thẳng SN là đường cao của ΔMNL.
hay SN ⊥ ML.