Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn:
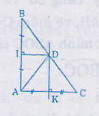
Từ hình vẽ ta có:
DK là trung trực của Ac, DI là đường trung trực của AB. Do đó ∆ADK = ∆CDK (c.c.c)
=> ˆADK=ˆCDKADK^=CDK^
hay DK là phân giác ˆADCADC^
=> ˆADKADK^ = 1212ˆADCADC^
∆ADI = ∆BDI (c.c.c)
=> ˆADI=ˆBDIADI^=BDI^
=> DI là phân giác ˆADBADB^
=> ˆADIADI^ = 1212 ˆADBADB^
Vì AC // DI ( cùng vuông góc với AB) mà DK ⊥ AC
=> DK ⊥ DI
hay ˆADKADK^ + ˆADIADI^ = 900
Do đó 1212ˆADCADC^ + 1212 ˆADBADB^ = 900
=> ˆADCADC^ + ˆADBADB^ = 1800

Từ hình vẽ ta có:
DK là trung trực của Ac, DI là đường trung trực của AB. Do đó ∆ADK = ∆CDK (c.c.c)
=> ˆADK=ˆCDKADK^=CDK^
hay DK là phân giác ˆADCADC^
=> ˆADKADK^ = 1212ˆADCADC^
∆ADI = ∆BDI (c.c.c)
=> ˆADI=ˆBDIADI^=BDI^
=> DI là phân giác ˆADBADB^
=> ˆADIADI^ = 1212 ˆADBADB^
Vì AC // DI ( cùng vuông góc với AB) mà DK ⊥ AC
=> DK ⊥ DI
hay ˆADKADK^ + ˆADIADI^ = 900
Do đó 1212ˆADCADC^ + 1212 ˆADBADB^ = 900
=> ˆADCADC^ + ˆADBADB^ = 1800

ta có:
DK là trung trực của Ac, DI là đường trung trực của AB. Do đó ∆ADK = ∆CDK (c.c.c)
=> gócADK = góc CDK
hay DK là phân giác góc ADC
=> góc ADK = 1/2 góc ADC
∆ADI = ∆BDI (c.c.c)
=> góc ADI = góc BDI
=> DI là phân giác góc ADB
=> góc ADI = 1/2 góc ADB
Vì AC // DI ( cùng vuông góc với AB) mà DK vuông góc AC
=> DK vuông góc DI
hay góc ADK + góc ADI = 90º
Do đó 1/2 góc ADC + 1/2 gócADB = 90 độ
=> góc ADC + góc ADB = 180 độ
=> góc BDC = 180º => góc BDC là góc bẹt .
=> B,C,D thảng hàng
tisck nha

cau 1 :
A B C E
Xet tam giac ABD va tam giac EBD co : BD chung
goc ABD = goc DBE do BD la phan giac cua goc ABC (gt)
AB = BE (Gt)
=> tam giac ABD = tam giac EBD (c - g - c)
=> goc BAC = goc DEB (dn)
ma goc BAC = 90 do tam giac ABC vuong tai A (gt)
=> goc DEB = 90
=> DE _|_ BC (dn)
b, tam giac ABD = tam giac EBD (cau a)
=> AB = DE (dn)
AB = 6 (cm) => DE = 6 cm
DE _|_ BC => tam giac DEC vuong tai E
=> DC2 = DE2 + CE2 ; DC = 10 cm (gt); DE = 6 cm (cmt)
=> CE2 = 102 - 62
=> CE2 = 64
=> CE = 8 do CE > 0

Sửa câu b: Từ M kẻ ME
Bg
a/ Xét hai tam giác AMB và AMC có:
AB = AC (gt)
BM = MC (vì M là trung điểm của BC)
AM là cạnh chung
Nên \(\Delta AMB=\Delta AMC\)(c.c.c)
Vậy \(\Delta AMB=\Delta AMC\)
b/ Xét hai tam giác vuông AME và AMF có:
\(\widehat{EAM}=\widehat{FAM}\)(vì \(\Delta AMB=\Delta AMC\))
AM là cạnh chung
Nên \(\Delta AME=\Delta AMF\)(g.c.g)
Do đó AE = AF (hai cạnh tương ứng)
Vậy AE = AF
c và d hơi dài. Đợi một thời gian :((

a, xét \(\Delta\)BEM và \(\Delta\)CFM có:
\(\widehat{B}\)=\(\widehat{C}\)(gt)
BM=CM(trung tuyến AM)
\(\Rightarrow\)\(\Delta\)BEM=\(\Delta\)CFM(CH-GN)
b,Ta có \(\Delta\)ABM=\(\Delta\)ACM(c.c.c)
\(\Rightarrow\)\(\widehat{BAM}\)=\(\widehat{CAM}\)
Gọi O là giao của AM và EF
xét tam giác OAE và tam giác OAF có:
AO cạnh chung
\(\widehat{OAE}\)=\(\widehat{OAF}\)(cmt)
vì AB=AC mà EB=FC nên AE=AF
\(\Rightarrow\)tam giác OAE=tam giác OAF(c.g.c)
\(\Rightarrow\)\(\widehat{AOE}\)=\(\widehat{AOF}\)mà 2 góc này ở vị trí kề bù nên\(\widehat{AOE}\)=\(\widehat{AOF}\)=90 độ(1)
\(\Rightarrow\)OE=OF suy ra O là trung điểm EF(2)
từ (1) và (2) suy ra AM là đg trung trực của EF
c, vì \(\widehat{BAM}\)=\(\widehat{CAM}\)=> AM là p/g của \(\widehat{BAC}\)(1)
ta có tam giác BAM=tam giác CAM(c.g.c)
=> AD là p/g của góc BAC(2)
từ (1) và(2) suy ra AM và AD trùng nhau nên A,M,D thẳng hàng
a, Ta có : Tam giác ABC cân tại A => Góc B=Góc C
Xét tam giác BEM vuông tại E và tam giác CFM vuông tại F
BM=CM (BM là trung tuyến)
Góc B=Góc C
=> Tam giác BEM=Tam giác CFM(ch-gn)
b,Từ a, \(\Delta\)BEM=\(\Delta CFM\)=> ME=MF (1);BE=FC
Mà AB=AC=> AE=AF(2)
Từ 1 và 2 => AM là trung trực của EF