Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dùng thước thẳng, dễ dàng đo được đoạn MN dài 1,5cm
\(\Rightarrow\left\{{}\begin{matrix}AB=2\cdot MN=2\cdot1,5=3\left(cm\right)\\CD=6\cdot MN=6\cdot1,5=9\left(cm\right)\end{matrix}\right.\)
Vậy \(\dfrac{AB}{CD}=\dfrac{3}{9}=\dfrac{1}{3}.\)

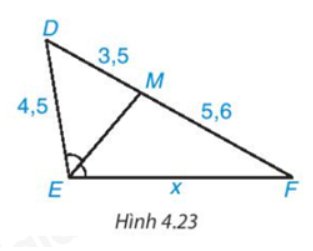
Trong Hình 4.23 có \(\widehat {DME} = \widehat {MEF}\) nên EM là tia phân giác của \(\widehat {{\rm{DEF}}}\).
Áp dụng tính chất đường phân giác của tam giác, ta có:
\(\dfrac{{E{\rm{D}}}}{{EF}} = \dfrac{{M{\rm{D}}}}{{MF}}\) hay \(\dfrac{{4,5}}{x} = \dfrac{{3,5}}{{5,6}}\)
Suy ra: \(x = \dfrac{{5,6.4,5}}{{3,5}} = 7,2\)(đvđd)
Vậy x = 7,2 (đvđd).

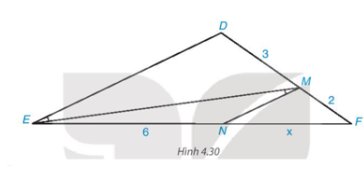
Trong Hình 4.30 có \(\widehat {DEM} = \widehat {EMN}\) mà hai góc này ở vị trí so le trong nên MN // DE.
Áp dụng định lí Thalès vào tam giác DEF có MN // DE, ta có:
\(\dfrac{{MF}}{{M{\rm{D}}}} = \dfrac{{NF}}{{NE}}\) hay \(\dfrac{2}{3} = \dfrac{x}{6}\)
Suy ra \(x = \dfrac{{2.6}}{3} = 4\) (đvđd).
Vậy x = 4 (đvđd).

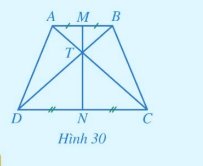
a, Xét \(\Delta ADC\)và \(\Delta BDC\)có:
DC là cạnh chung.
\(\widehat {ADC} = \widehat {BCD}\)(do ABCD là hình thang cân)
AD = BC
\( \Rightarrow \Delta ADC = \Delta BDC(c.g.c)\)
\( \Rightarrow \widehat {CAD} = \widehat {DBC}\)(2 góc tương ứng) hay
Do: \(\Delta ADC = \Delta BDC\)
Xét \(\Delta BAD\)và \(\Delta ACB\)có:
AB chung
AD = BC
AC = BD
\( \Rightarrow \Delta BDA = \Delta ACB\) (c.c.c)
\( \Rightarrow \widehat {BDA} = \widehat {ACB}\)(2 góc tương ứng) hay \(\widehat {TDA} = \widehat {TCB}\)
b, Xét \(\Delta TAD\)và \(\Delta TBC\)có:
\(\widehat {TAD} = \widehat {TBC}\)(theo câu a)
AD = BC (ABCD là hình thang cân)
\(\widehat {TDA} = \widehat {TCB}\)(theo câu a)
\( \Rightarrow \Delta TAD = \Delta TBC \Rightarrow TA = TB,TC = TD\)
c, Vì: TA = TB \( \Rightarrow \Delta ATB\)cân tại T suy ra TM là trung trực của AB
TC = TD \( \Rightarrow \Delta DTC\)cân tại T suy ra TN là trung trực của CD
Mà: M, T, N thẳng hàng. Nên MN là đường trung trực của cả 2 đường thẳng AB và CD

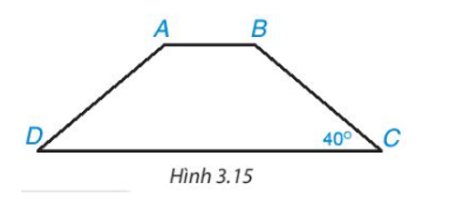
Hình thang cân ABCD (AB //CD) nên ta có:
\(\widehat A = \widehat B;\widehat C = \widehat D = {40^o}\)
\(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
Khi đó: \(\widehat A + \widehat A + {40^o} + {40^o} = {360^o}\)
Hay: \(2\widehat A + {80^o} = {360^o}\)
Suy ra: \(2\widehat A = {360^o} - {80^o} = {280^o}\)
Do đó: \(\widehat A = {140^o}\) nên \(\widehat B = {140^o}\)
Vậy: \(\widehat A = {140^o};\widehat B = {140^o};\widehat C = {40^o};\widehat D = {40^o}\)

Đáp án đúng là: C
Trong Hình 4.31 có \(\widehat {AMN} = \widehat {ABC}\) mà hai góc này ở vị trí đồng vị nên MN // BC.
Áp dụng định lí Thalès vào tam giác ABC, ta có:
\(\dfrac{{AM}}{{BM}} = \dfrac{{AN}}{{CN}}\) hay \(\dfrac{2}{3} = \dfrac{{1,5}}{x}\)
Suy ra \(x = \dfrac{{1,5.3}}{2} = 2,25\)
Vậy x = 2,25.

Lời giải
a)
Ta có \(\left\{{}\begin{matrix}MD=MB\\NA=NC\end{matrix}\right.\) \(\Rightarrow\)MN//DC
\(\Rightarrow\Delta OMN\approx\Delta ODC\approx OBA\)
Tỷ số đồng dạng
\(\dfrac{OM}{OD}=\dfrac{MN}{DC}=\dfrac{ON}{OC}\)\(\Rightarrow MN=\dfrac{OM}{OD}.DC=\dfrac{1}{4}.5,6=1,4\left(cm\right)\)
\(\dfrac{OM}{OB}=\dfrac{MN}{AB}\Rightarrow AB=\dfrac{OB}{OM}.MN=2MN=2,8\left(cm\right)\)
b)
\(\left\{{}\begin{matrix}CD=4MN\\AB=2MN\end{matrix}\right.\)
\(\Rightarrow\dfrac{CD-AB}{2}=\dfrac{4MN-2MN}{2}=MN\)

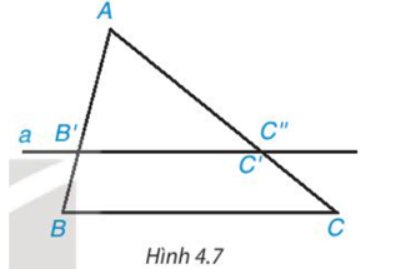
• Ta có \(\dfrac{{AB'}}{{AB}} = \dfrac{4}{6} = \dfrac{2}{3};\dfrac{{AC'}}{{AC}} = \dfrac{6}{9} = \dfrac{2}{3}\)
Do đó \(\dfrac{{AB'}}{{AB}} = \dfrac{{AC'}}{{AC}}\)
• Đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’ nên B’C’’ // BC.
Áp dụng định lí Thalès vào ∆ABC, ta có:
\(\dfrac{{AB'}}{{AB}} = \dfrac{{AC''}}{{AC}}\) hay \(\dfrac{4}{6} = \dfrac{{AC''}}{9}\)
Suy ra: \(AC'' = \dfrac{{4.9}}{6} = 6\)(cm).
Vậy AC’’ = 6 cm.
• Trên cạnh AC lấy điểm C’ sao cho AC’ = 6 cm.
Đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’ nên điểm C’’ nằm trên cạnh AC sao cho AC’’ = 6 cm.
Do đó, hai điểm C’, C’’ trùng nhau.
Vì hai điểm C’, C’’ trùng nhau mà B’C’’ // BC nên B’C’ // BC.

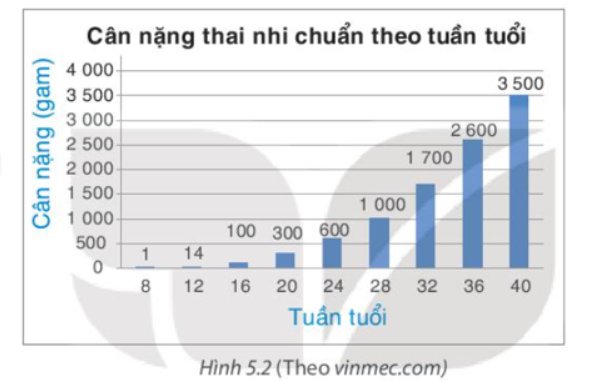
Từ biểu đồ trên, ta lập bảng thống kê:
Tuần tuổi | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
Cân nặng (gam) | 1 | 14 | 100 | 300 | 600 | 1 000 | 1 700 | 2 600 | 3 500 |
Ta có thể dùng biểu đồ đoạn thẳng để biểu diễn dữ liệu trên.
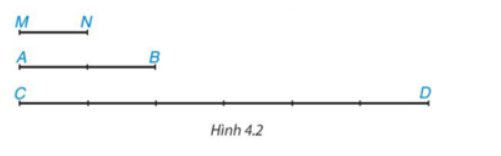



Chọn đoạn MN làm đơn vị độ dài thì MN = 1 (đvđd).
Khi đó, AB = 2 (đvđd); CD = 6 (đvđd).
Do đó \(\dfrac{{AB}}{{C{\rm{D}}}} = \dfrac{2}{6} = \dfrac{1}{3}\)
Vậy AB = 2 (đvđd); CD = 6 (đvđd); \(\dfrac{{AB}}{{C{\rm{D}}}} = \dfrac{1}{3}\)